Метод гармонического баланса.

Метод гармонического баланса базируется на замене нелинейного элемента системы линейным звеном, параметры которого определяются при гармоническом входном воздействии из условия равенства амплитуд первых гармоник на выходе нелинейного элемента и эквивалентного ему линейного звена. Метод является приближенным и может быть использован только в случае, когда линейная часть системы является фильтром низких частот, т.е. отфильтровывает все возникающие на выходе нелинейного элемента гармонические составляющие, кроме первой гармоники. При этом линейная часть может быть описана дифференциальным уравнением любого порядка, а нелинейный элемент может быть как однозначным, так и многозначным.

В основе метода гармонической линеаризации (гармонического баланса) лежит предположение, что на вход нелинейного элемента подается гармоническое воздействие с частотой ω и амплитудой А, т.е. x = А sinωt. В предположении, что линейная часть является фильтром низких частот, спектр выходного сигнала линейной части ограничивается только первой гармоникой, определяемой рядом Фурье (в этом и заключается приближенность метода, т.к. высшие гармоники выбрасываются из рассмотрения). Тогда связь между первой гармоникой выходного сигнала и входным гармоническим воздействием нелинейного элемента представляется в виде передаточной функции

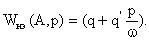
Уравнение (7.1) называется уравнением гармонической линеаризации, а коэффициенты q и q' - коэффициентами гармонической линеаризации, зависящие от амплитуды А и частоты ω входного воздействия. Для различных видов нелинейных характеристик коэффициенты гармонической линеаризации сведены в таблицу [2,4,13]. Следует заметить. что для статических однозначных коэффициент q'(А)=0. Подвергнув уравнение (7.1) преобразованию по Лапласу при нулевых начальных условиях с последующей заменой оператора p на jω (p = jω ), получим эквивалентный комплексный коэффициент передачи нелинейного элемента

Wнэ(jω,A) = q + jq'

После того, как проведена гармоническая линеаризация, для анализа и синтеза нелинейных САУ возможно применение всех методов, применяемых для исследования линейных систем, в том числе и использование различных критериев устойчивости. При исследовании нелинейных систем на основе метода гармонической линеаризации в первую очередь решают вопрос о существовании и устойчивости периодических (автоколебательных) режимов. Если периодический режим устойчив, то в системе существуют автоколебания с частотой ω0 и амплитудой А0. Рассмотрим нелинейную систему, включающую в себя линейную часть с передаточной функцией

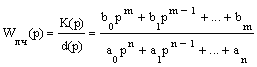
и нелинейный элемент с эквивалентным комплексным коэффициентом передачи (7.2). Расчетная структурная схема нелинейной системы приобретает вид

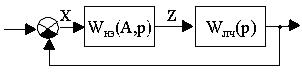
Для оценки возможности возникновения автоколебаний в нелинейной системе методом гармонической линеаризации необходимо найти условия границы устойчивости, как это делалось при анализе устойчивости линейных систем. Если линейная часть описывается передаточной функцией (7.3), а нелинейный элемент (7.2), то характеристическое уравнение замкнутой системы будет иметь вид

d(p) + k(p)(q(ω,A) + q'(ω,A)) = 0 (7.4)

На основании критерия устойчивости Михайлова границей устойчивости будет прохождение годографа Михайлова через начало координат. Из выражений (7.4) можно найти зависимость амплитуды и частоты автоколебаний от параметров системы, например, от коэффициента передачи k линейной части системы. Для этого необходимо в уравнениях (7.4) коэффициент передачи k считать переменной величиной, т.е. это уравнение записать в виде:

d(jω) + K(jω)(q(ω,A) + q'(ω,A)) = Re(ω0,A0,K) +Jm(ω0,A0,k) = 0 (7.5)

где ωo и Ao - возможные частота и амплитуда автоколебаний.

Тогда, приравнивая к нулю действительную и мнимую части уравнения (7.5)

можно построить границу устойчивости (D-разбиение) по интересующему нас параметру k (рис.7.6).

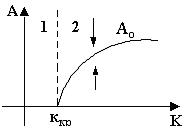
Анализируя рис.7.6 можно заключить, что в области 1 автоколебания невозможны и критический коэффициент равен ккр, а в области 2 колебания сходятся к величине амплитуды Ao и частоты ωo (автоколебательный режим) в зависимости от начальных условий. По графику рис.7.6 можно выбрать коэффициент передачи k, при котором амплитуда и частота возможных автоколебаний имеет допустимые значения или вообще отсутствует.

Чаще на практике используется графоаналитический метод определения возможных амплитуд и частот автоколебаний в нелинейных системах. В соответствии с критерием устойчивости Найквиста незатухающие колебания в линейной системе возникают в том случае, когда амплитудно-фазовая характеристика разомкнутой системы проходит через точку с координатами [ 1, j0]. Данное условие является также условием существования автоколебаний в гармонически линеаризованной нелинейной системе (рис.7.5), т.е.

1 + Wлч(jω)*Wнэ(jω,A)=0 (7.7)

или Wлч(jω)=-1/Wнэ(jω,A). (7.8)

Решение уравнения (7.8) относительно частоты и амплитуды автоколебаний можно получить графически, как точку пересечения годографа частотной характеристики линейной части системы Wлч(jω) и годографа обратной характеристики нелинейной части -1/Wнэ(jω,А) (рис7.7). Если эти годографы не пересекаются, то режим автоколебаний в исследуемой системе не существует.

Рис. 7.7. Годографы линейной и нелинейной частей системы

Для устойчивости автоколебательного режима с частотой ω0 и амплитудой А0 требуется, чтобы точка на годографе нелинейной части М, соответствующая увеличенной амплитуде А0+ ΔА по сравнению со значением в точке пересечения годографов, не охватывалась годографом частотной характеристики линейной части системы, в противном случае автоколебания неустойчивые. На рис. 7.7 дан пример расположения годографов для случая, когда в нелинейной системе существуют устойчивые автоколебания. Параметры автоколебаний на входе нелинейного элемента определяются в точке пересечения годографов: частота из Wлч(jω), а амплитуда из Wнэ-1(A). Исследование нелинейных систем возможно по логарифмическим частотным характеристикам (метод шаблонов) [2]. Метод гармонического баланса позволяет вести синтез нелинейных САУ на обеспечение требуемых показателей качества меняя параметры или линейной части, или нелинейного элемента.