Критерий устойчивости Михайлова

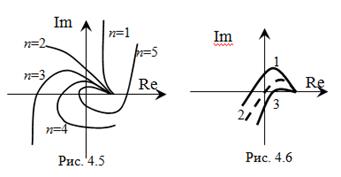
Для устойчивой системы годограф характеристического вектора порядка n, начинаясь на действительной положительной полуоси комплексной плоскости, при изменении ω от 0 до ∞ последовательно охватывает в положительном (против часовой стрелки) направлении n квадратов комплексной плоскости.

На рис. 4.5 представлены годографы устойчивых систем различных порядков. На рис. 4.6 показаны годографы устойчивой (график 1), неустойчивой (график 3) и нейтральной (график 2 проходит через начало координат – границу устойчивости) систем.

Пример. 4.3. Проанализируем устойчивость системы ФАПЧ из примера 4.2.

Перейдем от D(p) (4.11) к G(iω) (4.15):

U(ω)=a₀–ω²a₂ = 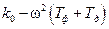, V(ω)=ω(a₁–a₃ω²)= 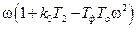. (4.20)

Из совместного решения уравнений U(ω) = 0, V(ω) = 0 получаем:

ω²_крIm= 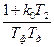, ω²_крRe= 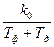; 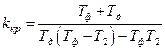. (4.21)

Как и следовало ожидать, значение k_крсовпало с (4.14).

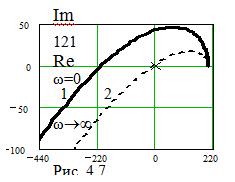
На рис. 4.7 приведены годографы устойчивых РАС при Т_ф = 0,1 с, Т_д= 5 мс,
k₀= 200 1/с (46,0 дБ).

График 1 построен при Т₂ = 4,7 мс (при Т₂ = 4,76 мс 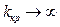). Для этого случая k_кр = 1,6×10⁴ (84,1 дБ), ω_крRe= 43,6 рад/с, ω_крIm=62,3 рад/с.

График 2 построен при Т₂ = 0. В этом случае k_кр=210 (46,4 дБ),
ω_крRe= 43,6 рад/с, ω_крIm= 44,7 рад/с. В этом случае запас устойчивости мал (менее 0,5 дБ), и годограф проходит очень близко к критической точке (0,0).

Таким образом, подтвердились сделанные ранее выводы (пример 4.2) о влиянии Т₂форсирующего звена на устойчивость РАС.

Анализируя годографы замкнутых систем, можно установить такое следствие из критерия устойчивости Михайлова.

Если найти все корни уравнений U(ω) = 0 (ω_кр1, ω_кр3,…, ω_кр2k-1), V(ω)=0 (ω_кр0, ω_кр2,…, ω_кр2k), то ω_крj должны последовательно перемежаться (ω_кр2k-1< ω_2k).

С помощью этого следствия можно обойтись без построения годографа. Для этого достаточно вычислить корни (ω_крj) уравнения V(ω) = 0, а затем найти значения U(ω) в точках ω_крj– U(ω_крj).

Если знаки U(ω_крj) с ростом jчередуются, то система будет устойчивой.

Если есть хотя бы один участок, на котором не будет чередования знаков, – система неустойчива.

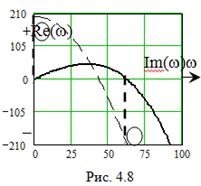
На рис. 4.8 показано применение данного следствия на примере 4.3. Мнимая часть (V(ω)) имеет 2 корня, знаки соответствующих значений U(ω) различны, следовательно, система будет устойчивой.

16.Принцип действия и функциональная схема системы ЧАП, и ЧАП с преобразованием частоты:

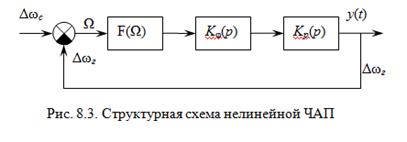
Структурная схема ЧАП с преобразованием частоты приведена на рис. 3.3 и описана в линейном режиме в п. 3.2. Построим структурную схему ЧАП (рис. 8.3) с учетом нелинейности характеристики дискриминатора F(Ω) (см. рис. 3.4).

В анализе примем, что нестабильностью частоты ГУН можно пренебречь. Примем, что 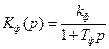; ; 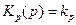W – отклонение частоты на выходе ЧАП (частота ГУН, промежуточная частота) в установившемся режиме от номинального значения (остаточная расстройка).

Составим уравнение работы ЧАП относительно отклонения частоты.

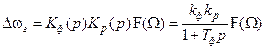. (8.2)

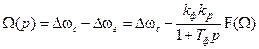. (8.3)

Будем считать, что ЧАП работает в режиме стабилизации частоты (сигналом воздействия является частота эталонного генератора w_эт).

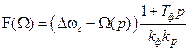. (8.4)

Решим уравнение (8.4) для стационарного режима (t ® ¥ или p ® 0). В этом случае 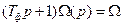и уравнение сводится к виду

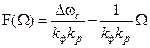. (8.5)

Для наглядности решим уравнение (8.5) графически.

Правая часть (8.5) представляет собой уравнение прямой относительно переменной W.

Решением будут являться точки пересечения (точки 1, 2, 3 на рис. 8.4) этой прямой и графика дискриминационной характеристики F(Ω).

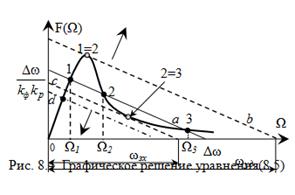
Полученные решения Ω₁, Ω₂, Ω₃ для общего случая (спло­ш­ная прямая a на рис. 8.4) необходимо проанализировать на локальную устойчивость.

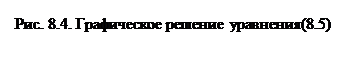Есть несколько способов. Воспользуемся простейшим [2]: линеаризацией характеристики в области каждой точки решения
( ):

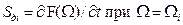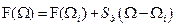. (8.6)

Подстановка (8.6) в (8.4) после замены переменных дает :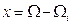

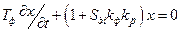. (8.7)

Решение (8.7) и анализ устойчивости [2] приводят к следующим условиям устойчивости решений:

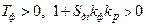. (8.8)

В точке 1 крутизна характеристики S_д1 > 0 и условие устойчивости (8.8) выполняется. В точке 2 S_д2 < 0 и 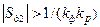– условие (8.8) не выполняется и система неустойчива. В точке 3 S_д3 < 0, но 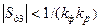, поэтому условие (8.8) выполняется и система устойчива.

Система не может находиться в точке 2, она должна перейти в устойчивое состояние – точку 1 или 3.

В зависимости от начальной расстройки Δω_c (возможные изменения показаны стрелочками на рис. 8.4) уравнение (8.5) может иметь одно или два решения.

Двум решениям на рис. 8.4 соответствуют штриховые линии b и c. Штриховая линия b позволяет определить по точке пересечения с осью абсцисс полосу захвата (при этом точки 1 и 2 сливаются), а штриховая линия c – полосу удержания (при этом сливаются точки 2 и 3) [24].

Рабочая полоса ЧАП – полоса захвата (точки 1 на рис. 8.4).

Полоса удержания не может быть меньше, чем полоса захвата.

Одному решению, которое получается при нахождении начальной расстройки в полосе захвата, на рис. 8.4 соответствует штрихпунктирная линия d [24].

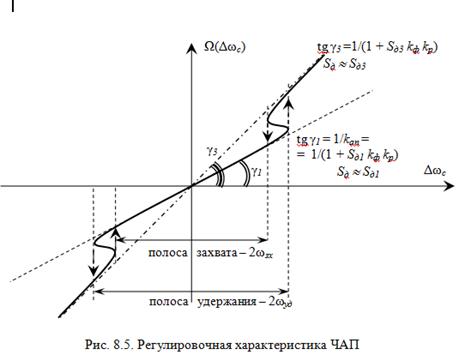
Зависимость остаточной расстройки Ω от начальной Δω_с называется регулировочной характеристикой и является наиболее информативной характеристикой ЧАП (рис. 8.5) (k_ап = 1 + S_д k_ф k_р).

Система ЧАП является статической РАС с конечной ошибкой 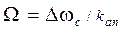(k_ап = 1 + S_д k_ф k_р – коэффициент автоподстройки).

Пусть при включении ЧАП находится в асинхронном режиме, в этом случае начальная расстройка Δω_с находится вне полосы удержания (Δω_с > ω_уд ), частота ГУН равна некоторой собственной частоте (частота при разомкнутой петле ОС). При медленном изменении частоты эталонного генератора в сторону уменьшения рассогласования частот, как только расстройка Δω_с окажется в полосе захвата (Δω_с < ω_зх ), ЧАП войдет в режим слежения (синхронизм, рабочий режим) за частотой сигнала (в режиме стабилизации – за частотой эталонного генератора). При этом частота ГУН меняется скачком и ее отличие от ω_э уменьшается в k_ап раз, в результате частота ГУН почти равна частоте эталонного генератора.

Если теперь начать увеличивать расстройку Δω_с , ЧАП будет работать в синхронном режиме до тех пор, пока значение расстройки будет оставаться внутри полосы удержания (Δω_с < ω_уд ). Чтобы вывести ЧАП из синхронного режима, потребуется увеличить расстройку так, чтобы она оказалась вне полосы удержания (Δω_с > ω_уд ).

Если при включении ЧАП начальная расстройка окажется в полосе захвата (Δω_с < ω_зх ), то система сразу входит в синхронизм.

Если при включении ЧАП начальная расстройка будет лежать в интервале между полосой захвата и удержания ( ω_зх < Δω_с< ω_уд ), то достоверно поведение предсказать нельзя, так как система перейдет в одно из рассмотренных ранее устойчивых состояний.

Максимальная корректирующая расстройка Δω_{k max} , вырабатываемая системой ЧАП, соответствует точке (1 = 2) на рис. 8.4 и равна

Δω_{k max} = k_рS_дU_{д max}, (8.9)

где U_{д max} – максимальное напряжение на выходе дискриминатора.

Соотношение между полосой захвата и удержания оценивается следующими формулами:

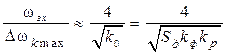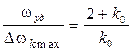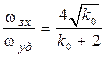; ; . (8.10)

Точность системы прямо пропорциональна k_ап , поэтому для уменьшения установившейся ошибки k_ап следует увеличивать. Однако при этом, как следует из формул (8.10), уменьшается полоса захвата, а значит, уменьшается рабочий диапазон частот эффективной автоподстройки. Таким образом, в статической ЧАП есть противоречие между точностью и полосой эффективной автоподстройки. Для разрешения данного противоречия используют астатическую ЧАП.

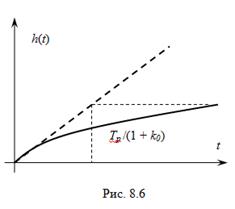В переходном режиме поведение ошибки будет зависеть в основном от характеристики фильтра. Для данного случая 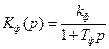, поэтому 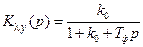, и остаточная расстройка будет изменяться не скачком, а плавно с некоторой задержкой.

На рис. 8.6 приведена ПХ для этого случая.

Время регулирования оценивается формулой .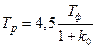

Применение системы ЧАП в РПрмУ по сравнению с ФАПЧ имеет достоинство: ЧАП не реагирует на «зеркальную помеху».

17.Принцип действия и функциональная схема системы ФАПЧ:

Функциональная схема ФАПЧ приведена на рис. 3.6, а на рис. 3.7 приведена ее структурная схема, сведенная к обобщенному виду. Работа линеаризованной системы ФАПЧ в режиме стабилизации частоты описана в п. 3.3.

Проанализируем работу ФАПЧ в режиме стабилизации частоты с учетом нелинейности дискриминационной характеристики. Будем считать, что начальная фаза опорного (эталонного) генератора φ₀ = 0, возмущение x(t) отсутствует, а нестабильностью частоты эталонного генератора и ГУН можно пренебречь.

Принципиальным отличием статической характеристики ФД является ее периодичность. Для непрерывных (аналоговых) систем ФАПЧ статическая характеристика представляет собой «синусоиду». В импульсных и цифровых системах характеристика ФД имеет другие формы.

ФД выполняет перемножение сигналов эталонного генератора ГУН.

За основу примем уравнение ФАПЧ (3.9):

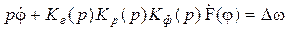. (8.11)

Пусть К_г(р) = 1 , К_р(р) = k_р ; 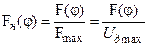– нормированная характеристика дискриминатора.

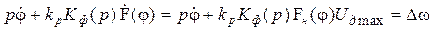. (8.12)

Рассмотрим сначала работу системы ФАПЧ при отсутствии фильтра (К_ф(р) = 1). В этом случае уравнение (8.12) преобразуется к виду

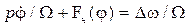, (8.13)

где 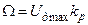– максимальная корректирующая расстройка, которая в данном случае имеет смысл полосы удержания ω_уд.

Если рассмотреть стационарный режим, то приходим к уравнению статики

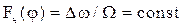. (8.14)

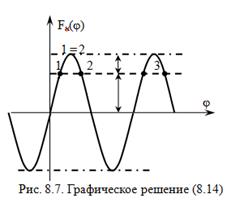
На рис. 8.7 показано графическое решение уравнения (8.14).

Считаем, что 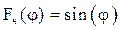. Штриховая прямая 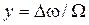пересекает график F_н(j) в двух точках на периоде.

Анализ полученных решений на устойчивость, приведенный в [2, 24], показывает, что точки пересечения с графиком F_н(j), которые находятся на участках с 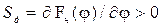соответствуют устойчивому состоянию (точки 1 и 3), а точки, находящиеся на участках с отрицательной крутизной дискриминационной характеристики 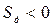, – неустойчивому состоянию (точки 2 и 4).

Штрихпунктирная прямая на рис. 8.7 (точки 1 и 2, а также 3 и 4 сливаются) соответствует пределам рабочего участка (j = ±0,5p + pn), который определяет полосу захвата ФАПЧ.

Точка 1 находится на участке
(j < ±0,5p), который приближенно считается линейным в линеаризованной системе ФАПЧ (п. 3.3).

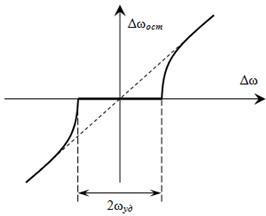
На рис. 8.8 приведена регулировочная характеристика (зависимость остаточной расстройки от начальной) для ФАПЧ при отсутствии фильтра.

В отличие от ЧАП, регулировочная характеристика ФАПЧ имеет область (полоса удержания 2ω_уд), в которой установившаяся ошибка равна нулю. Таким образом, система ФАПЧ является астатической по частоте, а по фазе имеет некоторый постоянный фазовый сдвиг.

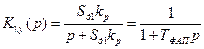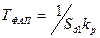. ( ) (8.15)

При отсутствии фильтра полосы захвата и удержания совпадают.

Если расстройка Δω находится в полосе удержания, то ФАПЧ находится в режиме синхронизма, в котором частота ГУН устанавливается равной частоте эталонного генератора (ω_г = ω_э ) с точностью до фазы.

Если увеличивать начальную расстройку Δω так, чтобы она вышла из полосы удержания, то ФАПЧ перейдет в режим биений.

В режиме биений напряжение на выходе дискриминатора не постоянно, а периодически изменяется; фаза сигнала неограниченно нарастает, частота ГУН периодически колеблется вокруг частоты сигнала.

Положительные и отрицательные полуволны периода имеют разную длительность, поэтому кроме переменной составляющей на выходе ФД появляется и постоянная составляющая.

Для возвращения ФАПЧ в рабочий режим необходимо уменьшить расстройку Δω так, чтобы она вернулась в полосу удержания. По мере уменьшения Δω будет увеличиваться доля постоянной составляющей на выходе ФД и уменьшаться частота биений.

При вхождении ФАПЧ в синхронизм ФД будет иметь только постоянную составляющую, величина и полярность которой будут зависеть от величины и знака начальной расстройки.

Проанализируем теперь работу ФАПЧ с ФНЧ первого порядка (например, интегрирующая RC-цепь 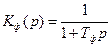из прил. 2).

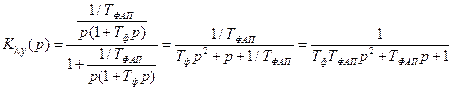, (8.16)

где .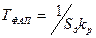

Получилось уравнение второго порядка, которое удобно свести к стандартному виду:

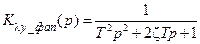, (8.17)

где , .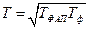

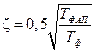Уравнение ФАПЧ (8.12) в данном случае запишется в виде.

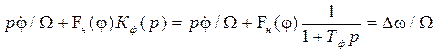. (8.18)

После преобразований получим:

,

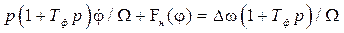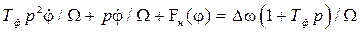. (8.19)

На рис. 8.9 приведена типичная регулировочная характеристика для данного случая.

При малой постоянной времени фильтра Т_ф (это эквивалентно его широкой полосе пропускания) полоса захвата ω_зх имеет почти тот же размер, что и полоса удержания ω_уд.

С увеличением постоянной времени Т_ф улучшаются фильтрирующие свойства системы по отношению к сигналу, но в то же время уменьшается полоса захвата системы.

Уменьшение полосы захвата можно объяснить так. При су­щест­венной начальной рас­строй­ке на выходе ФД существуют колебания с частотой начальной расстройки, которые ослабляются ФНЧ. В результате максимально возможное напряжение на входе ГУН получается меньше, чем в рассмотренном выше случае, в котором ФНЧ отсутствовал [24].

При значительных постоянных времени ФНЧ ( 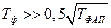) отношение полос захвата и удержания оценивается формулой [24].

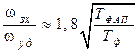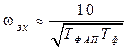, . (8.20)

Кроме того, при выборе Т_ф следует учитывать характер (z) и время регулирования переходного процесса РАС.

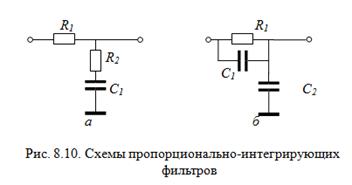
Для уменьшения данного противоречия необходимо скорректировать характеристики фильтра. Наиболее простое решение – применение пропорционально-интегрирующего фильтра (ПИФ).

На рис. 8.10 представлены возможные схемы ПИФ.

ПФ ПИФ определяется формулой

,

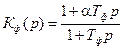где Т_ф = (R₁ + R₂) C₁ , a = R₁ /(R₁ + R₂)для схемы рис. 8.10а; Т_ф = R₁ (C₁ + C ₂), a = C₁ (C₁ + C ₂) для схемы рис. 8.10б.

На рис. 8.11 представлена регулировочная характеристика для системы ФАПЧ с ПИФ.

Штриховыми стрелочками на рис. 8.11 для сравнения показана полоса захвата при использовании интегрирующего RC-фильтра, рас­смот­ренного выше.

Введение ПИФ обеспечивает увеличение запаса РАС по фазе.

Рассмотрим работу нелинейной ФАПЧ при различных величинах начальной расстройки Δω.

Пусть при включении начальная расстройка Δω находится в полосе захвата, в этом случае ФАПЧ находится в синхронном режиме, в котором частота ГУН устанавливается равной частоте эталонного генератора с точностью до фазы.

Если увеличивать начальную расстройку Δω так, чтобы она вышла из полосы удержания, то ФАПЧ прекратит нормальную работу и перейдет в режим биений [24].

Для возвращения ФАПЧ в рабочий режим необходимо уменьшить расстройку Δω так, чтобы она вернулась в полосу захвата. По мере уменьшения Δω будет увеличиваться доля постоянной составляющей на выходе ФД и уменьшаться частота биений.

Если при включении ФАПЧ в синхронизм ФД расстройка Δω будет находиться вне полосы захвата, но в полосе удержания (ω_зх < Δω < ω_уд ), то достоверно поведение ФАПЧ предсказать нельзя: она может перейти как в синхронный, так и в асинхронный режимы.

Так как системы ЧАП и ФАПЧ имеют свои достоинства и недостатки, представляет интерес применение комбинированных РАС, в которых за счет объединения работы ФАПЧ и ЧАП удается получить существенное улучшение качества работы [24].

18. Принцип действия системы автоматической регулировки управления:

Система автоматической регулировки усиления (АРУ) предназначена для обеспечения малых изменений уровня сигнала на выходе усилительного тракта при существенных изменениях уровня сигнала на его входе без искажений формы сигнала. Уровень входного сигнала радиоприемных устройств (РПрмУ) непрерывно изменяется по многим причинам: из-за изменения расстояния между источником излучения и РПрмУ, из-за изменения условий распространения радиоволн, а в радиолокации к этим причинам добавляются флуктуации эффективной отражающей поверхности цели, смена целей и т. д.

Динамический диапазон изменения входных сигналов РПрмУ может достигать 60–100 дБ, при этом для нормальной работы оконечных каскадов и выходных устройств РПрмУ желательно получить диапазон изменения выходных сигналов не более 10–20 дБ. В противном случае может появиться перегрузка, которая не только приводит к искажениям передаваемой информации, но и может на значительное время вызвать полную потерю чувствительности РПрмУ.

По характеру выполняемых задач АРУ делятся на три группы: инерционные, безынерционные и программные.

Инерционные АРУ следят за изменением среднего уровня входного сигнала и применяются обычно в вещательных РПрмУ.

Безынерционные АРУ следят за изменением мгновенного значения амплитуды входного сигнала и применяются обычно в радиолокации.

Программные АРУ имеют заранее заданный закон регулирования и используются обычно при приеме импульсных сигналов с известным, периодически повторяющимся распределением уровней во времени.

АРУ могут быть построены по принципу прямого, обратного и комбинированного регулирований.

В АРУ с прямым регулированием (прямая АРУ) коэффициент усиления (КУ) регулируемого усилителя (РУ) определяется его входным сигналом и не зависит от его выходного сигнала. Структурная схема прямой АРУ приведена на рис. 3.8.

Регулирующее напряжение U_p(t) формируется с помощью петли регулирования АРУ (рис. 3.8), которая состоит из усилителя АРУ (У) и детектора. Вход петли регулирования АРУ подключен ко входу регулируемого РУ, поэтому U_p формируется из входного сигнала РУ. Усилитель АРУ осуществляет предварительное усиление входного сигнала U_вх(t), детектор АРУ выделяет амплитуду усиленного входного сигнала и формирует пропорциональное ей регулирующее напряжение U_p(t).

Детекторы АРУ в качестве нагрузки имеют ФНЧ, которые придают АРУ необходимую инерционность, обусловленную как соображениями устойчивости, так и условием отсутствия демодуляции АМ-сигналов.

КУ РУ зависит от величины регулирующего напряжения U_p(t), подаваемого на управляющий вход РУ: чем больше U_p,тем меньше КУ.

При возрастании U_вх возрастает и U_p, формируемое петлей регулирования АРУ, в результате КУ РУ уменьшается, что приводит к замедлению роста амплитуды выходного сигнала U_вых.

В прямой АРУ при больших КУ РУ амплитуда U_вых может даже уменьшаться с увеличением амплитуды U_вх.

На рис. 3.9 приведены примеры амплитудной характеристики U_вых = f(U_вх) РУ прямой АРУ (графики 2–4).

График 1 на рис. 3.9 соответствует амплитудной характеристике РУ при отключенной АРУ.

График 2 соответствует случаю идеального регулирования, когда величина U_вых постоянна и не зависит от изменений величины U_вх при превышении порогового значения U_А. Идеальная амплитудная характеристика обычно достигается при определенном КУ усилителя АРУ, близком к КУ РУ.

При недостаточном КУамплитудная характеристика при U_вх > U_А приобретает вид возрастающей линии (график 3), так как U_вых РУ возрастает с увеличением U_вх, хотя медленнее, чем при отсутствии петли АРУ (график 1).

При избыточном КУамплитудная характеристика при U_вх > U_А приобретает вид спадающей линии (график 4), а U_вых уменьшается с увеличением U_вх.

Таким образом, прямая система АРУ может обеспечить идеальное регулирование, но для этого следует обеспечить стабильность КУ усилителя АРУ, который должен быть большим, что приводит к усложнению cxeмы АРУ.

Кроме того, АРУ с прямым регулированием непосредственно не контролирует амплитуду U_вых РУ. Следовательно, АРУ с прямым регулированием не может компенсировать изменения амплитуды U_вых, вызванные нестабильностью параметров РУ или воздействиями помех на РУ, и поэтому в чистом виде на практике не используется.

В АРУ с обратным регулированием (обратная АРУ)КУ РУопределяется его выходным сигналом.