Обобщенная структурная система следящей РАС

Многие следящие РАС, рассмотренные ниже, могут быть сведены к обобщенной структурной схеме, которая представлена на рис. 3.1.

Функциональные устройства РАС, указанные в обобщенной схеме, включают устройства измерения сигнала ошибки и корректирующие устройства, предназначенные для создания необходимых динамических характеристик, управляющее устройство и объект управления.

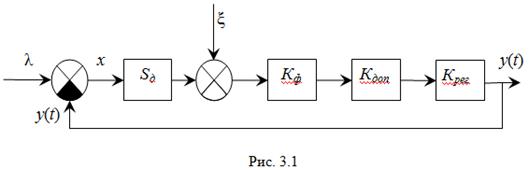
Работа РАС происходит в условиях действия различных помех, что учитывается введением возмущающего воздействия ξ(t), которое учитывает изменение регулировочных характеристик РАС из-за изменений условий окружающей среды, нестабильности источников питания и т. п.

В обобщенной РАС дискриминатор считается безынерционным и описывается параметром F(x) = S_д (крутизной дискриминационной характеристики).

Остальные элементы обобщают математические модели корректирующего устройства, устройства управления и элемента управления.

После преобразований данную схему можно упростить до обобщенной схемы, показанной на рис. 3.2 (K₁ = S_д, K₂ = К_ф К_доп К_рег).

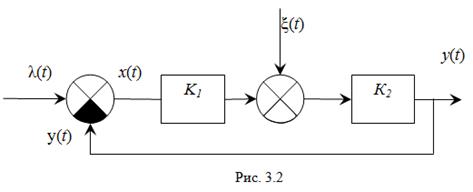
Порядок астатизма типовой следящей системы равен числу интеграторов v, включенных в контур управления.

Для задания №4, приведенного в [6], примем следующие ПФ звеньев РАС:

; ; .

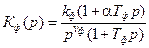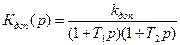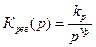7.Устойчивость линеаризованных непрерывных систем. Основные сведения об устойчивости

На любую РАС в процессе работы действуют различные возмущения, которые могут нарушить ее нормальную работу. Возникает вопрос об устойчивости системы к любым внешним воздействиям и возмущениям.

В простейшем случае понятие устойчивости связано со способностью системы с определенной точностью возвращаться в состояние равновесия (невозмущенное состояние) после исчезновения внешних возмущений, которые вывели РАС из этого состояния.

Различают устойчивость состояния равновесия и устойчивость движения. Считается, что строгое определение устойчивости было дано А. М. Ляпуновым в 1892 г. [10]. В упрощенной форме условие устойчивости сформулируем так.

Пусть y(t) – траектория возмущенного движения, y₀(t) – траектория невозмущенного движения, а при t = 0 y(t) – y₀(t) = δ(0).

В произвольный момент времени t_i y(t_i) – y₀(t_i) = δ(t_i).

Если при всех t > 0 |y(t) – y₀(t)| ≤ δ(0), а также |y(t_i) – y₀(t_i)| < δ(t_i-1), то динамическая система будет устойчивой.

Система асимптотически устойчива, если при t → ∞ область притяжения стягивается в точку: .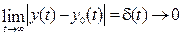

Если система является устойчивой при любых возмущениях, то говорят о глобальной устойчивости.

Если вопрос об устойчивости в точке зависит от характера нелинейности и величины возмущений, то речь идёт о локальной устойчивости.

Динамика линеаризованной системы описывается уравнением

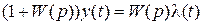, (4.1)

где W(p) – ПФ разомкнутой системы.

(a₀pⁿ + a_n-1p^n-1 + . . . + a_n) y(t) = (b₀p^m + b_m-1p^m-1 +. . . + b_m) l(t) . (4.2)

Решение уравнения y(t) = y_св(t) + y_вын(t) есть сумма свободной и вынужденной 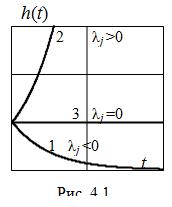составляющих. Свободная составляющая у_св(t) – это решение однородного дифференциального уравнения.

a_npⁿ + a_n-1p^n-1 + . . . + a₀ = 0 . (4.3)

Известно, что для полинома n-го порядка существует n корней (в общем случае комплексных) l₁, l₂,…, l_n. Тогда полином (4.3) можно записать в виде

a_n(p – l₁)(p – l₂)(p – l₃). . .(p – l_n) = 0 . (4.4)

Для того, чтобы сделать вывод об устойчивости системы, необходимо определить характер переходного процесса.

Из дисциплины «Высшая математика» известно, что свободная составляющая y_св(t) описывает переходный процесс системы:

y_св(t) = 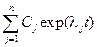. (4.5)

Пусть корень λ_j вещественный. Если λ_j < 0, то аргумент экспоненты в (4.5) отрицательный, переходный процесс будет иметь затухающий характер (график 1 на рис. 4.1). При λ_j > 0 аргумент экспоненты в (4.5) положительный и переходный процесс будет иметь нарастающий характер (график 2 на рис. 4.1). При λ_j = 0 экспонента превратится в константу (график 3 на рис. 4.1).

Корни, имеющие мнимые части, образуют комплексно-сопряженные пары: p_i = α_i + iβ_i, p_i+1 = α_i – iβ_i. Вещественная часть корней соответствует экспоненте в (4.6), мнимая часть – комбинации гармоник (синусов и косинусов) с циклической частотой w = β_i :

y_св(t) = 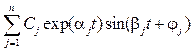. (4.6)

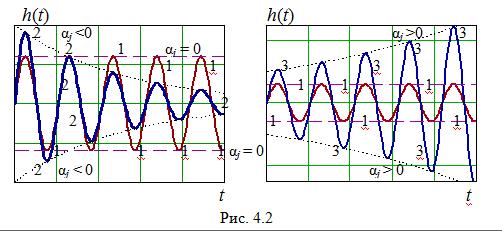
На рис. 4.2 представлены графики колебательных переходных процессов для вещественных частей (4.6) различных знаков: график 1 – α_j = 0 (постоянные колебания с w = β_i), график 2 – затухающий переходный процесс (α_j < 0), график 3 – нарастающий переходный процесс (α_j > 0).

Из проведенного анализа следует, что система будет устойчива, если корни характеристического уравнения лежат в левой комплексной полуплоскости. Если среди корней есть хотя бы один правый корень, то система неустойчива. Если корень имеет нулевую действительную часть, то система будет на границе устойчивости: нейтральной при λ_j = 0 (β_i = 0 → a₀ = 0) или колебательной (β_i ¹ 0).

Предположим, что все корни левые. Подставим это условие в (4.4). После приведения подобных к виду (4.3) получим важный вывод о положительности коэффициентов a_j характеристического полинома.

Необходимое условие устойчивости – все коэффициенты характеристического полинома (4.3) должны быть больше нуля. Решение о достаточности условия зависит от значений корней полинома.

Пример 4.1.

1. 4р⁵ + 16р⁴ + 8р² + р + 12 = 0 – система неустойчива, так как коэффициент при р³ равен нулю.

2. 14р³ – 7р² + 2р + 4 = 0 – система неустойчива, так как коэффициент при р² отрицательный.

3. р⁵ + 7р⁴ + 8р³ + 9р² + 4р + 2 = 0 – необходимое условие устойчивости выполняется, для определения устойчивости РАС необходимо найти корни полинома. (С помощью «Mathcad» можно проверить, что в данном случае все корни лежат в левой комплексной полуплоскости, значит, система будет устойчивой. )

Для сложных РАС порядок уравнений может быть значительным, и вычисление корней характеристического полинома оказывается затруднительным.

Устойчивость можно оценить, не прибегая к вычислениям корней, с использованием алгебраических и графоаналитических критериев, которые были разработаны во времена, когда не было компьютеров. Хотя в настоящее время вычисление корней характеристического полинома даже больших порядков трудностей не представляет, эти критерии не потеряли актуальности.

К алгебраическим относится критерий А. Гурвица, к частотным относятся критерии А. В. Михайлова, Г. Найквиста и др.