Запасы устойчивости: нормы ,, способы определения, связь с параметрами качества системы

Отклонение критической величины от номинальной называется запасом устойчивости.

Запасы устойчивости определяются на частоте среза (запас устойчивости по фазе j_з) и критической частоте (запас устойчивости по усилениюА_з).

Запас устойчивости по усилению (4.27) определяет, во сколько раз необходимо увеличить коэффициент усиления разомкнутой РАС, чтобы она оказалась на границе устойчивости.

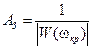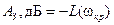или . (4.27)

Запас устойчивости по фазе (4.28) показывает, на какое значение ФЧХ (ЛФЧХ) разомкнутой РАС на частоте среза отличается от p±pn (180°±360°n).

или 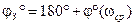. (4.28)

Для нормальной работы РАС обычно требуется запас устойчивости по усилению не менее 2 (6 дБ), а запас по фазе – порядка 40–60°.

Если φ₃ ≥ 90˚, то переходный процесс имеет апериодический характер, а при φ₃ < 30° получается колебательная ПХ.

13. Критерий устойчивости Гурвица

Для уравнения (4.3) a_npⁿ+a_n-1p^n-1+ . . .+ a₀ =0 составляется матрица Гурвица:

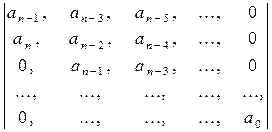. (4.7)

Порядок составления матрицы Гурвица (4.7) такой: по главной диагонали с верхнего левого угла до правого нижнего записываются с убыванием индексов коэффициенты с a_n-1 по a₀. Над элементами главной диагонали записываются коэффициенты с убывающими индексами, а под элементами главной диагонали – с возрастающими.

Для оценки устойчивости необходимо вычислить определители Гурвица, которые получаются из (4.7) путем вычеркивания равного числа строк и столбцов в левом верхнем углу матрицы:

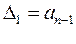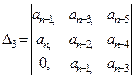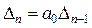, , , . (4.8)

Система будет устойчива, если все определители Гурвица при a_n> 0 – положительные.

Если определитель ∆_n= 0, то система находится на границе устойчивости.

Возможны два случая: a_n= 0 или ∆_n–1 = 0.

Если a_n= 0, это соответствует нейтрально-устойчивой системе.

Если определитель ∆_n-1= 0, это соответствует колебательной границе устойчивости.

Из условия ∆_n-1 = 0 можно определить параметры, при которых РАС находится на границе устойчивости. Это позволяет вычислить критические параметры (например, постоянные времени звеньев, коэффициент усиления по постоянному току k_кр), соответствующие границе устойчивости. Отклонение критической величины от номинальной называется запасом устойчивости.

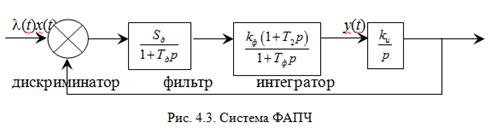
Пример. 4.2. Рассмотрим линеаризованную систему ФАПЧ (рис. 4.3) при отсутствии внешнего возмущения (S_д – крутизна характеристики дискриминатора, Т₂– постоянная времени форсирующего звена).

K_λy(p) = 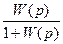, где W(р) – передаточная функция разомкнутой системы:

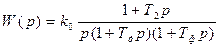, (4.9)

где 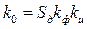– коэффициент передачи разомкнутой системы по постоянному току. Зная W(р) (4.9), найдем ПФ замкнутой системы.

K_λy(p) = 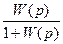= 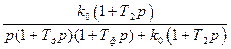. (4.10)

Характеристическое уравнение, которое также можно было получить с помощью формулы (4.1), имеет вид

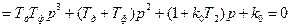. (4.11)

Определяем коэффициенты характеристического полинома a_n :

а₃= Т_дТ_ф, а₂= Т_д+ Т_ф, а₁= 1 + k₀Т₂, а₀= .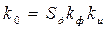

Составляем матрицу Гурвица:

.

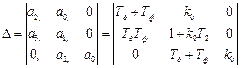Находим определители Гурвица:

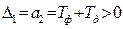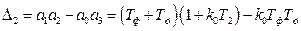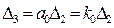, , . (4.12)

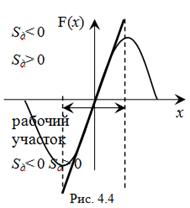В данном примере а₁, а₂, а₃> 0, но а₀зависит от S_д (k_и > 0, k_ф > 0), которая на разных участках дискриминационной характеристики различна (рис. 4.4). Вне рабочего (линейного) участка S_д< 0 и система неустойчива. На рабочем участке S_д> 0 и необходимое условие устойчивости выполняется.

Достаточное условие устойчивости требует анализа D₂:

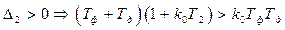, (4.13)

что в итоге позволяет найти критический коэффициент усиления k_кр:

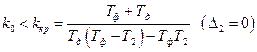. (4.14)

Система будет устойчива, если k₀<k_кр.

Если форсирующее звено в фильтре отсутствует (Т₂= 0), то .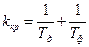

Если Т₂ увеличивается, то k_кр также повышается, значит, устойчивость системы увеличивается. Таким образом, в данной РАС введение форсирующего звена повышает устойчивость системы.

Приравняв нулю знаменатель (4.14), получим, что 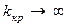при 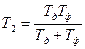, то есть в этом случае система будет устойчива при любых k₀.

Для анализа устойчивости САУ с характеристическим полиномом выше пятой степени применяют модификацию критерия Гурвица – критерий П. Льенара – Р. Шипара [10], который можно сформулировать так.

Если все коэффициенты характеристического полинома положительны (a_j> 0), то достаточное условие устойчивости сводится к тому, чтобы положительными были все определители Гурвица либо четного (D₂, D₄,.., D_2k), либо нечетного индекса (D₁, D₃,.., D_2k-1). (Доказано, что из положительности D_2k следует положительность D_2k-1 [10].)

В результате количество определителей Гурвица, которые необходимо вычислить, существенно уменьшается.

14. Критерий устойчивости Найквиста

На практике более широко применяется критерий Г. Найквиста, который позволяет судить об устойчивости замкнутой РАС по частотным характеристикам разомкнутой системы.

Пусть разомкнутая РАС устойчива и не содержит идеальных интеграторов.

Выражение (4.22) отражает связь ПФ разомкнутой и замкнутой систем:

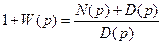. (4.22)

Поскольку у реальных РАС порядок полинома числителя N(p) не может превышать порядок полинома знаменателя D(p), порядки полиномов D(p) и D(p) + N(p) будут одинаковы.

Проанализируем характеристический вектор

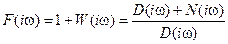. (4.23)

Числитель (4.23) является характеристическим вектором замкнутой системы, а знаменатель – разомкнутой системы.

Пусть характеристическое уравнение замкнутой системы имеет m правых корней (n– m – число левых корней), а характеристическое уравнение разомкнутой системы – l правых корней (n – l – число левых корней). Изменение аргумента вектора F(iω) при изменении ω от –∞ до +∞ составит

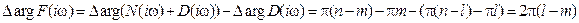.(4.24)

Для устойчивой замкнутой системы m = 0.

Следовательно, при изменении ω от 0 до ∞

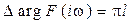. (4.25)

Если РАС устойчива в разомкнутом состоянии (l=0), то .

Таким образом, если разомкнутая и замкнутая системы устойчивы, то изменение аргумента вектора F(iω) равно нулю, следовательно, его годограф не охватывает начало координат.

Если годограф F(iω) охватывает начало координат, то система в замкнутом состоянии неустойчива.

От годографа F(iω) удобно перейти к годографу разомкнутой системы W(iω). Если в разомкнутом положении система устойчива, тогда в замкнутом состоянии она также будет устойчива, если годограф Найквиста начинается на действительной полуоси ЧПФ и при изменении ω от 0 до ∞ не охватывает критическую точку(–1, i0).

Если точка (–1, i0) охватывается, то система в замкнутом состоянии будет неустойчива. Если кривая проходит через точку (–1, i0), то система нейтральна (находится на границе устойчивости).

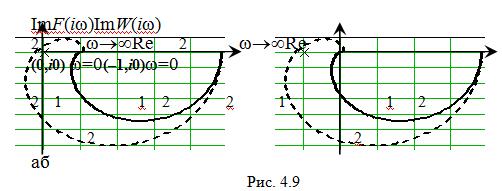
На рис. 4.9 показаны годографы F(iω) (рис. 4.9а) и W(iω) (рис. 4.9б)

устойчивых (график 1) и неустойчивых (график 2) в замкнутом состоянии систем.

Если РАС неустойчива в разомкнутом состоянии (l¹0), то для оценки устойчивости системы в замкнутом состоянии существует правило переходов Я. З. Цыпкина: для того, чтобы система, неустойчивая в разомкнутом состоянии, была устойчива в замкнутом состоянии, необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов годографа через отрезок вещественной оси слева от критической точки (]–∞, –1[ для W(iω)) была равнаl/2 (l – число правых корней разомкнутой системы).

Для годографа W(iω) при изменении ω от 0 до ∞ переход вещественной оси ]–∞, –1[ называется положительным, если он происходит сверху вниз, и отрицательным, если он происходит снизу вверх.

Если РАС содержит v идеальных интеграторов в контуре управления, то начальное значение ФЧХ равно –vp/2, а АЧХ – бесконечности. Для оценки устойчивости таких систем в замкнутом состоянии их дополняют дугой –vp/2 бесконечного радиуса, которая соединяет уходящую в бесконечность линию годографа с положительной вещественной полуосью (рис. 4.10). Критерий Найквиста в этом случае применяется к результирующему графику.

Если годографы W(iω) пересекают вещественную ось только справа от критической точки (–1, i0), такие РАС называют абсолютно устойчивыми.

Если система теряет устойчивость не только при повышении коэффициента усиления, но и при его уменьшении (рис. 4.10в), то такая система называется условно устойчивой [1].

На рис. 4.10 приведены годографы W(iω) для систем, которые содержат один идеальный интегратор (дуга R=¥ будет иметь размер 1хp/2, то есть 90°).

На рис. 4.10а построен годограф для системы ФАПЧ из примера 4.2, разомкнутая ЧПФ для которой

, (4.26)

а Т₂ = 4,7 мс (k₀<<k_кр). Так как результирующий график не охватывает точку (–1, i0), система в замкнутом состоянии будет абсолютно устойчивой, что подтверждает сделанные ранее выводы.

На рис. 4.10б представлен годограф той же системы при Т₂ = 0, k₀ = 2 k_кр. В этом случае в замкнутом состоянии система будет неустойчивой, так как результирующий график охватывает критическую точку (–1, i0).

На рис. 4.10в показан более сложный случай, когда годограф W(iω) пересекает вещественную полуось ]–∞, –1[ дважды: один переход положительный, второй – отрицательный, значит, разность числа переходов равна нулю (l/2=0). Следовательно, система в замкнутом состоянии будет условно устойчивой.