L-критерий тенденций Пейджа
Критерий L Пейджа применяется для сопоставления показателей, измеренных в трех и более условиях на одной и той же выборке испытуемых.
Критерий позволяет выявить тенденции в изменении величин признака при переходе от условия к условию. Его можно рассматривать как продолжение теста Фридмана, поскольку он не только констатирует различия, но и указывает на направление изменений.
Критерий позволяет проверить наши предположения об определенной возрастной или ситуативно обусловленной динамике тех или иных признаков. Он позволяет объединить несколько произведенных замеров единой гипотезой о тенденции изменения значений признака при переходе от замера к замеру. Если бы не его ограничения, критерий был бы незаменим в «продольных», или лонгитюдинальных, исследованиях.
К сожалению, имеющиеся таблицы критических значений рассчитаны только на небольшую выборку (n ≤ 12) и ограниченное количество сопоставляемых замеров (с ≤ 6).
В случае, если эти ограничения не выполняются, приходится использовать критерий χ2r Фридмана, рассмотренный в предыдущем параграфе.
В критерии L применяется такое же ранжирование условий по каждому испытуемому, как и в критерии χ2r. Если испытуемый в первом опыте допустил 17 ошибок, во втором – 12, а в третьем – 5, то 1-й ранг получает третье условие, 2-й ранг – второе, а 3-й ранг – первое условие. После того, как значения всех испытуемых будут проранжированы, подсчитываются суммы рангов по каждому условию. Затем все условия располагаются в порядке возрастания ранговых сумм: на первом месте слева окажется условие с меньшей ранговой суммой, за ним – условие со следующей по величине ранговой суммой, и т. д., пока справа не окажется условие с самой большой ранговой суммой. Далее мы с помощью специальной формулы подсчета L проверяем, действительно ли значения возрастают слева направо. Эмпирическое значение критерия L отражает степень различия между ранговыми суммами, поэтому, чем выше значение L, тем более существенны различия.
Гипотезы
H0: Увеличение индивидуальных показателей при переходе от первого условия ко второму, а затем к третьему и далее, случайно.
H1: Увеличение индивидуальных показателен при переходе от первого условия ко второму, а затем к третьему и далее, неслучайно.
При формулировке гипотез мы имеем в виду новую нумерацию условий, соответствующую предполагаемым тенденциям.
Ограничения критерия Пейджа
1. Нижний порог – 2 испытуемых, каждый из которых прошел не менее 3-х замеров в разных условиях. Верхний порог – 12 испытуемых и 6 условий (n ≤ 12, с ≤ 6). Критические значения критерия L предусматривают три уровня статистической значимости: р ≤ 0,05; р ≤ 0,01; р ≤ 0,001.
2. Необходимым условием применения теста является упорядоченность столбцов данных: слева должен располагаться столбец с наименьшей ранговой суммой показателей, справа – с наибольшей. Можно просто пронумеровать заново все столбцы, а потом вести расчеты не слева направо, а по номерам, но так легче запутаться.
Пример.Продолжим рассмотрение примера с анаграммами. В таблице 12.8 показатели времени решения анаграмм и их ранги представлены уже в упорядоченной последовательности: анаграмма 1, анаграмма 3, анаграмма 2. Действительно ли время решения увеличивается при такой последовательности предъявления анаграмм?
Таблица 12.8
Показатели времени решения анаграмм 1, 3, 2 и их ранги (n = 5)
| Код имени испытуемого | Условие 1. Анаграмма 1 | Условие 2. Анаграмма 3 | Условие 3. Анаграмма 2 | ||||
| Время (сек) | Ранг | Время (сек) | Ранг | Время (сек) | Ранг | ||
| Л-в | |||||||
| П-о | |||||||
| К-в | |||||||
| Ю-ч | |||||||
| Р-0 | |||||||
| Суммы | |||||||
| Средние | 10,2 | 9,4 |
АЛГОРИТМ
Подсчет критерия тенденций L Пейджа
1. Проранжировать индивидуальные значения первого испытуемого, полученные им в 1-м, 2-м, 3-м и т. д. замерах. При этом первым может быть любой испытуемый, например, первый по алфавиту имен.
2. Проделать то же самое по отношению ко всем другим испытуемым.
3. Просуммировать ранги по условиям, в которых осуществлялись замеры. Проверить совпадение общей суммы рангов с расчетной суммой.
4. Расположить все условия в порядке возрастания их ранговых сумм в таблице.
5. Определить эмпирическое значение L по формуле:
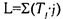 ,
,
где Tj – сумма рангов по данному условию;
j – порядковый номер, приписанный данному условию в упорядоченной последовательности условий.
6. По таблице 6 приложения 1 определить критические значения L для данного количества испытуемых n и данного количества условий с. Если Lэмп равен критическому значению или превышает его, тенденция достоверна.
Приступим к решению. Сумма рангов составляет: 6 + 9 + 5 = 30. Расчетная сумма:
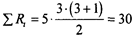
Реально полученная и расчетная суммы совпадают, мы можем двигаться дальше.
Как видно из таблицы 12.8, среднее время решения анаграммы 3 даже меньше, чем анаграммы 1. Однако мы исследуем не среднегрупповые тенденции, а степень совпадения индивидуальных тенденций. Нам важен именно порядок, а не абсолютные показатели времени. Поэтому и формулируемые нами гипотезы – это гипотезы о тенденциях изменения индивидуальных показателей.
Сформулируем гипотезы
H0: Тенденция увеличения индивидуальных показателей от первого условия к третьему является случайной.
H1: Тенденция увеличения индивидуальных показателен от первого условия к третьему не является случайной.
Эмпирическое значение L определяется по формуле:
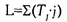 ,
,
где Тj – сумма рангов по каждому условию;
j – порядковый номер, приписанный каждому условию в новой последовательности.
Lэмп = (6 ∙ l) + (9 ∙ 2) + (15 ∙ 3) = 69.
По таблице 6 приложения 1 определяем критические значения L для данного количества испытуемых: n=5, и данного количества условий: с = 3.
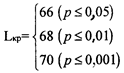 .
.
Построим «ось значимости».
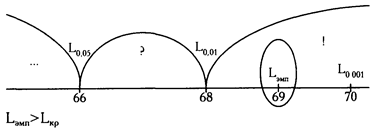
Ответ: H0 отклоняется. Принимается H1. Тенденция увеличения индивидуальных показателей от первого условия к третьему не является случайной (р < 0,01). Последовательность анаграмм: 1 (КРУА), 3 (ИНААМШ), 2 (АЛСТЬ) – будет в большей степени отвечать замыслу экспериментатора о постепенном возрастании сложности задач, чем первоначально применявшаяся последовательность.
Дата добавления: 2021-11-16; просмотров: 1152;











