Критерий устойчивости Найквиста

Этот критерий был получен Н. Найквистом в 1932 году для проверки усилителей с отрицательной обратной связью, а затем обобщен на системы автоматического управления.

Критерий Найквиста позволяет определить устойчивость системы с обратной связью (замкнутой системы) по экспериментально снятой или полученной на основе передаточной функции амплитудно-фазовой частотной характеристике разомкнутой системы (рис. 5.10).

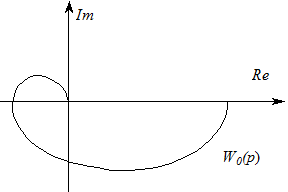
Рис. 5.10 - АФХ разомкнутой системы

Будем полагать, что известна передаточная функция разомкнутой системы

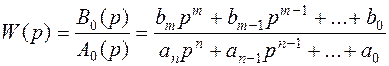, m≤n. (5.22)

Здесь 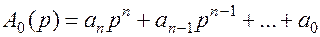- ее характеристический полином.

Структурная схема замкнутой системы имеет вид

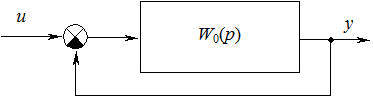
Рис. 5.11 - Структурная схема замкнутой системы

Передаточная функция замкнутой системы следующая:

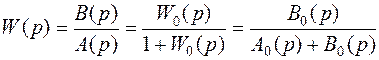, (5.23)

где 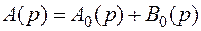- характеристический полином замкнутой системы.

Для получения критерия устойчивости вводится вспомогательная функция:

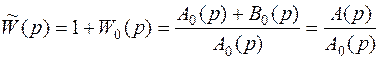. (5.24)

Как видим, числитель вспомогательной передаточной функции представляет собой характеристический полином замкнутой системы, а знаменатель - характеристический полином разомкнутой системы. Так как 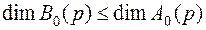, то в выражении для A(p)порядок суммы полиномов равен 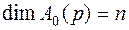. Следовательно, во вспомогательной передаточной функции 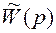полиномы числителя и знаменателя имеют один порядок (n).

В выражении (5.24) заменим р на jω и получим:

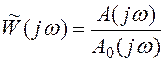. (5.25)

Рассмотрим результирующий угол поворота вектора 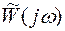при изменении ω от 0 до ∞, используя те же соотношения, что и при доказательстве критерия Михайлова.

Если замкнутая система устойчивая, то общее приращение фазы числителя (5.25) определяется как

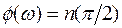. (5.26)

При устойчивой разомкнутой системе фаза в знаменателе будет иметь вид

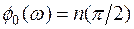. (5.27)

Результирующий угол поворота вектора 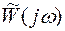равен разности (5.26) и (5.27).

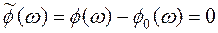. (5.28)

Таким образом, для устойчивости замкнутой системы (при устойчивой разомкнутой) должно выполняться соотношение (5.28). Это свойство имеет простую геометрическую интерпретацию: вспомогательная частотная характеристика не должна охватывать начало координат. Так как 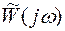отличается от 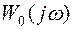на единицу, то можно строить амплитудно-фазовую характеристику разомкнутой системы, что значительно проще.

Формулировка критерия Найквиста. Для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика устойчивой разомкнутой системы при изменении ω от 0 до ∞ не охватывала точку с координатами {-1, j0}.

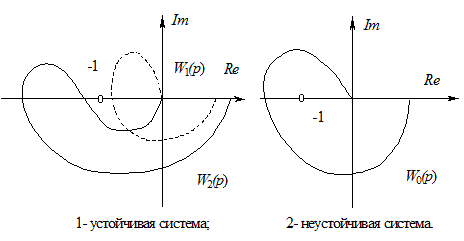
Рис. 5.12 - Частотные характеристики системы для критерия Найквиста

Разомкнутая система может быть неустойчива, но это не означает, что неустойчивой будет и замкнутая система. В этом случае меняется формулировка критерия Найквиста. Для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика неустойчивой разомкнутой системы при изменении ω от 0 до ∞ охватывала точку с координатами {-1 j0} в положительном направлении r/2 раз, где r - число корней характеристического уравнения разомкнутой системы с положительной вещественной частью.

Критерий Найквиста можно также применять, если разомкнутая система имеет в своем составе интегратор, т.е. ее передаточная функция следующая:

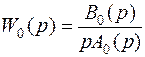. (5.29)

Полученная в результате замены р на jω в выражении (5.29) амплитудно-фазовая характеристика будет иметь неопределенность в точке ω= 0. Поэтому при ее построении делают аппроксимацию: характеристику дополняют полуокружностью бесконечно большого радиуса так, чтобы она начиналась на положительной вещественной полуоси (рис. 5.13).

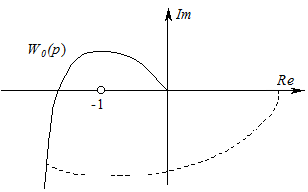
Рис. 5.13 - АФХ разомкнутой системы с интегратором

Замкнутая система будет находиться на границе устойчивости, если при некоторой частоте ω=ω₀ АФХ разомкнутой системы пересекает точку с координатами {-1, j0}. Аналитически условие границы устойчивости записывается в виде:

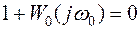. (5.30)