Условие устойчивости линейных систем

В случае стационарной линейной или линеаризованной системы устойчивость определяется только ее структурой и параметрами и не зависит от внешних воздействий. Если к системе РА приложено задающее воздействие – z(t) = g(t) и возмущающее воздействие (возмущение) – x(t) = f(t), то система уравнений в общем случае будет выглядеть так

(5.1)

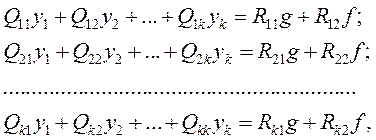
где Q_ij=Q_ij(p); R_ij=R_ij(p) – линейные дифференциальные операторы с постоянными коэффициентами, некоторые из них могут равняться нулю, y_i=y_i(p) – выходные величины элементов системы РА (параметры напряжений управления).

Система уравнений для стационарной системы может быть сведена к одному уравнению относительно одной из координат (чаще всего рассматривают уравнение САР для управляющего напряжения):

(5.2)

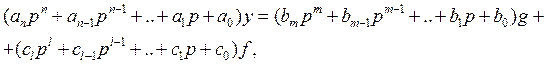
где y=y(t) – регулируемая величина;

g=g(t) – задающее воздействие;

f=f(t) – возмущающее воздействие;

a, b, c – постоянные коэффициенты;

n≥m и n≥l;

р – оператор Лапласа.

Для оценки устойчивости необходимо исследовать свободную составляющую решения уравнения (5.2), или решение однородного уравнения

(5.3)

.

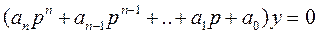Общим решением однородного уравнения (5.3) является сумма частных решений, которые определяются значениями корней характеристического уравнения

(5.4)

.

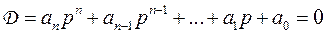Коэффициенты уравнения (5.4) зависят только от параметров системы, способа соединения и параметров составляющих систему звеньев.

Каждому вещественному корню α_i соответствует частное решение вида

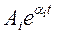. (5.5)

Каждому вещественному корню α_i кратности k соответствует k частных решений вида

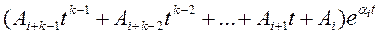. (5.6)

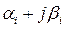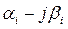Каждой паре комплексных сопряженных корней и соответствует два частных решения вида

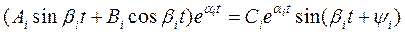(5.7)

(в частном случае α_i может быть равно нулю).

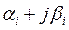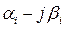Каждой паре комплексных сопряженных корней кратности k и соответствует 2k частных решений вида

(5.8)

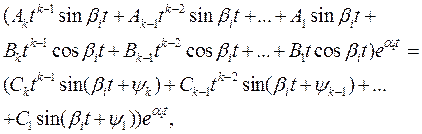
где 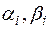- постоянные величины, а ( 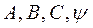) - постоянные интегрирования - всегда ограничены по абсолютной величине и зависят только от параметров системы, способа соединения и параметров, составляющих систему звеньев (аналогично коэффициентам характеристического уравнения), и определяются из системы алгебраических уравнений, составленных на основании начальных условий.

Если характеристическое уравнение системы радиоавтоматики не имеет кратных корней (что весьма вероятно), тогда корни вычисляют приближенно, и решение характеристического уравнения (5.4) согласно (5.5), (5.7) будет иметь только слагаемые вида:

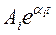и 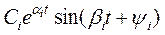. (5.9)

Пример.Пусть корни характеристического уравнения α₁, α₂ – кратности 2, α₃+jβ₃, α₃-jβ₃, (α₄+jβ₄ и α₄-jβ₄) – кратности 3. Тогда свободная составляющая регулируемой величины

.

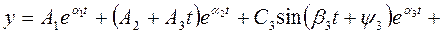
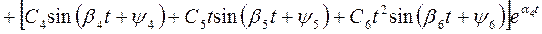Из решения уравнения (5.4) видно, что при неограниченном возрастании одного из слагаемых, неограниченно возрастает по абсолютной величине и вся сумма, независимо от наличия членов с разными знаками (5.6). Поэтому присутствие одного положительного вещественного корня α_i > 0 достаточно для того, чтобы соответствующее ему слагаемое в решении уравнения (5.4) неограниченно возрастало по абсолютной величине. При наличии пары сопряженных комплексных корней с положительной вещественной частью в решении уравнения (5.34) появляется гармоническое слагаемое (5.7) с неограниченно возрастающей амплитудой. В обоих случаях система оказывается неустойчивой.

Следовательно, для того чтобы линейная или линеаризованная система РА была устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения имели отрицательную вещественную часть. Система РА будет неустойчива, если решение характеристического уравнения системы РА имеет хотя бы один корень с положительной вещественной частью. Если при решении характеристического уравнения будет хотя бы один нулевой корень α_i=0, либо пара чисто мнимых корней (jβ_i)(-jβ_i), и при этом все остальные корни будут иметь отрицательную вещественную часть, значит система находится на границе устойчивости, и решение уравнения (5.4) будет иметь постоянную величину A_i, или гармоническую составляющую с постоянной амплитудой.

В случае линеаризованной системы при наличии нулевых или чисто мнимых корней, об устойчивости системы можно судить только после исследования ее нелинейных уравнений.

Как и любое комплексное число, корни характеристического уравнения можно представить в виде точек на комплексной плоскости (рис. 5.3).

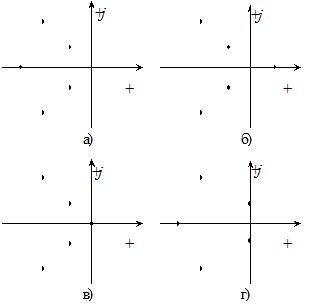
Рис. 5.3 - Расположение корней характеристического уравнения пятого порядка для устойчивой (а), неустойчивой (б) систем, систем находящейся на границе устойчивости (г) и систем, находящихся на границе

устойчивости при a₀=0 (в)

По виду графика корней характеристического уравнения легко судить об устойчивости системы. Для устойчивости линейной или линеаризованной системы необходимо и достаточно, чтобы все точки (корни характеристического уравнения) лежали в левой полуплоскости (рис. 5.3, а). В данном случае мнимая ось является границей устойчивости, если на мнимой оси находится один или несколько корней, то система находится на границе устойчивости (рис. 5.3, в, г), первый случай будет иметь место при a₀=0. Если один или несколько корней находятся в правой полуплоскости графика, то система неустойчива (рис. 5.3, б).

Вычисление корней характеристического уравнения реальной системы большого порядка весьма проблематично, поэтому были разработаны некие правила, основанные на приведенных выше вычислениях и называемые критериями устойчивости, которые позволяют оценивать устойчивость системы, не вычисляя корней характеристического уравнения.

Системы первого и второго порядка устойчивы, если все коэффициенты a₀, a₁…a_n характеристического уравнения (5.4) положительны. Для систем более высокого порядка положительность коэффициентов является необходимым, но не достаточным условием устойчивости. Если все коэффициенты характеристического уравнения положительные, то все его вещественные корни будут отрицательными, но среди комплексных корней могут быть и корни с положительной вещественной частью. Если хотя бы один из коэффициентов отрицательный, система заведомо неустойчива. При равенстве нулю коэффициента a₀ система находится на границе устойчивости, при равенстве нулю коэффициента a_i при i¹0 система находится на границе устойчивости, или неустойчива.

Пример.Оценить устойчивость системы первого порядка, передаточная функция которой имеет вид:

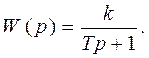
Решение. Характеристическое уравнение 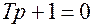имеет только один корень 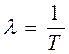, который будет отрицательным при Т > 0.

Следовательно, положительность коэффициентов характеристического уравнения для системы первого порядка является необходимым и достаточным условием устойчивости.

Пример.Получить условия устойчивости для системы 2-го порядка:

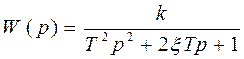
Решение. Запишем ее характеристическое уравнение

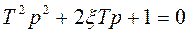
и определим корни:

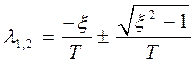
Они будут иметь отрицательную вещественную часть, когда знаки коэффициентов 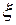и Т совпадают.

Таким образом, положительность коэффициентов характеристического уравнения для системы 2-го порядка также является необходимым и достаточным условием устойчивости.