Логарифмическая форма критерия Найквиста

Для проверки устойчивости замкнутой системы можно использовать логарифмические частотные характеристики разомкнутой, которые строятся почти без вычислений. Правила построения ЛАЧХ см. п.3.5. с. 33.

Формулировка критерия Найквиста. Для замкнутой системы необходимо и достаточно, чтобы на частотах, где ЛАЧХ положительна (т.е. L(ω) > 0), фазовая частотная характеристика разомкнутой системы не пересекала ось - 180⁰ или пересекала ее четное число раз.

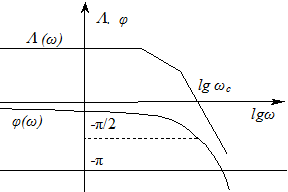
Рис. 5.14 - Логарифмические частотные характеристики,

иллюстрирующие критерий Найквиста

Замкнутая система будет находиться на границе устойчивости, если на той же частоте, где L(ω)=0, фазовая частотная характеристика разомкнутой системы пересекает ось – 180^о.

Области и запасы устойчивости

Основные понятия и определения

Поскольку при составлении математической модели делается ряд допущений, то параметры реальной системы несколько отличаются от расчетных (номинальных). Кроме того, с течением времени они могут изменяться в некотором диапазоне, но при этом свойство устойчивости должно сохраняться. Поэтому для нормальной работы система должна обладать определенным запасом устойчивости.

Рассмотрим линейную стационарную систему общего вида, описываемую системой уравнений (5.1) и соответствующее ей характеристическое уравнение (5.4), которое имеет n корней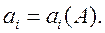

Определение. Областью устойчивости по параметрам будем называть множество матриц A, для которых выполняется общее условие устойчивости: .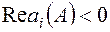

На практике обычно речь идет об изменении одного - двух параметров системы.

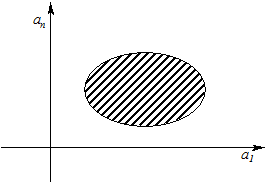
Рис. 5.15 - Область устойчивости системы

Определение. Критическими (граничными) будем называть такие значения матриц A, при которых система находится на границе устойчивости: Re λ(A)=0.

Определение. Запасом устойчивости называется диапазон значений параметра от номинального до граничного.