Критерий устойчивости Гурвица
Критерий устойчивости Гурвица находит широкое применение при анализе систем третьего и четвертого порядков, когда известны параметры системы. Кроме того, он позволяет получить аналитическое выражение (выражения) для границ области возможных значений какого-либо параметра (параметров) системы, при которых сохраняется устойчивое состояние системы.
Это алгебраический критерий, который предполагает рассмотрение характеристического уравнения (5.4) в стандартной форме
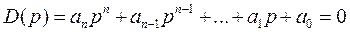 .
.
Из его коэффициентов по следующему правилу составляется матрица Гурвица: на главной диагонали сверху вниз вписываются коэффициенты характеристического уравнения от an-1 до a0 включительно. В каждом столбце вниз от диагонали записывают коэффициенты при возрастающих степенях оператора Лапласа - р, вверх - при убывающих степенях р. Недостающие элементы в столбце заполняются нулями. Либо в каждой строке справа от главной диагонали располагаются коэффициенты при убывающих через одну степенях p, слева от главной диагонали располагаются коэффициенты при возрастающих через одну степень оператора Лапласа p - ( 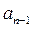 ,
, 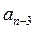 ,
, 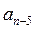 ,…).
,…).
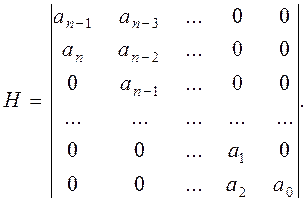 (5.10)
(5.10)
dim H=n × n. Приведем без доказательства критерий Гурвица.
Формулировка критерия. Для устойчивости линейной системы необходимо и достаточно, чтобы при an>0 все n определителей, получаемых из матрицы Гурвица Н, были положительны.
Где 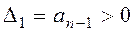 ;
;
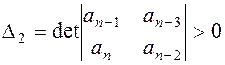 ;
;
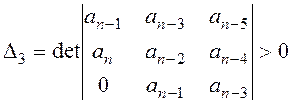 ; (5.11)
; (5.11)
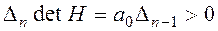 .
.
Условие границы устойчивости согласно критерию Гурвица имеет вид:
|
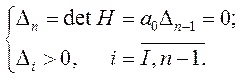
Пример.Оценить устойчивость системы 3-го порядка, передаточная функция которой имеет вид
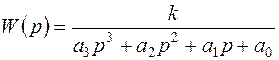 .
.
Запишем характеристическое уравнение согласно (5.4)
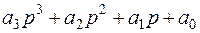
и составим матрицу Гурвица для этой системы 3го порядка (5.10)
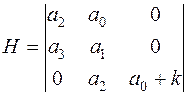 .
.
Условия устойчивости системы в соответствии с критерием Гурвица и (5.11) следующие:
1) 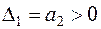 ;
;
2) 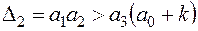 ;
;
3) 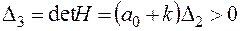 или
или 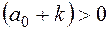 .
.
Поскольку положительность всех коэффициентов характеристического уравнения следует из необходимого условия, то условие устойчивости системы 3-го порядка принимает вид:
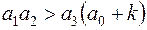 .
.
Дата добавления: 2020-10-25; просмотров: 555;











