Нахождение дифференциального уравнения САР по заданным передаточным функциям САР
В формуле 4.17 уберём знаменатель в правой части (перемножить левую и правую части на знаменатель). Тогда получим:
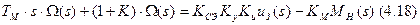
Уравнение (4.18) связывает изображение Лапласа угловой скорости и изображения Лапласа задающего напряжения и момента нагрузки.
Совершим обратное преобразование Лапласа для получения дифференциального уравнения.
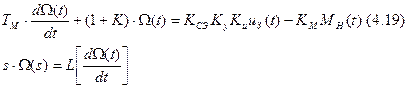
Преобразование справедливо для нулевых начальных условий!
По этой же методике можно найти разностное уравнение для дискретных систем.
Надо найти другую формулу, где должно учитываться ненулевое начальное условие Ω1. Если начальные условия ненулевые, то преобразование Лапласа от первой производной будет равно:
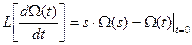
В нашем случае:
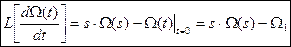
Для второй производной:
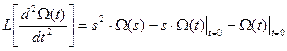
Чтобы получить новую формулу, надо опять осуществить прямое преобразование уравнения (4.19) с учётом начальных условий.
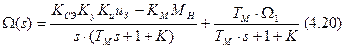
Опять воспользуемся таблицами соответствий между функциями времени и изображениями Лапласа (строки 5 и 4).
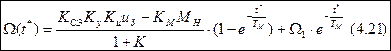
Достроим кривую (см. рис. 1).
Чтобы найти t1, надо открыть модель сравнивающего элемента. Оно начинается, когда uЗ – uТГ = uСТ/KСЭ.
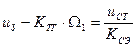
Находим отсюда Ω1. И потом подставляя в формулу для первого интервала это значение, находим t1.
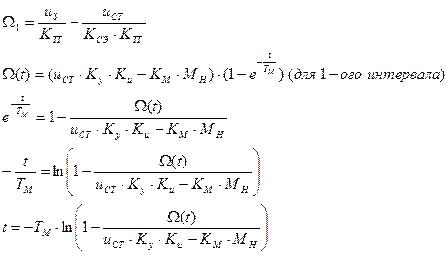
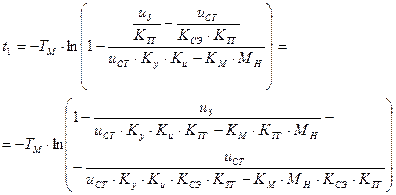
Дата добавления: 2020-10-25; просмотров: 514;











