Построение кривых переходного процесса в линейных стационарных непрерывных САР

Анализ системы – это изучение поведения управляемых переменных во время переходных и установившихся процессов (режимов). При этом задаётся структура системы, её параметры и входные воздействия на неё.

Наиболее сложной задачей является нахождение переходных импульсных функций, характеризующих поведение системы в переходных режимах.

Существует несколько основных способов построения кривых переходного процесса:

1) использование преобразования Лапласа входных и выходных функций времени (в случае САР угловой скорости речь идёт об использовании преобразования Лапласа для двух входных воздействий – u_З и M_Н, а выходная величина - Ω).

2) классические способы решения дифференциальных уравнений; для этого надо располагать общим дифференциальным уравнением всей системы.

3) численные способы решения дифференциальных уравнений с помощью персональных компьютеров, например, метод Адамса, (метод Рундекута в MATLAB?).

Самым простым является первый способ. С ним произошло ознакомление, когда рассматривались передаточные функции в изображениях Лапласа отдельных элементов. Но там рассматривался случай, когда были нулевые начальные условия. Этот способ усложняется, когда начальные условия ненулевые.

Рассмотрим построение кривой переходного процесса первым способом в статической САР угловой скорости. В момент пуска имеют место нулевые начальные условия, т.е. Ω = 0. Это справедливо только для системы САР угловой скорости, потому что в дифференциальном уравнении используется только первая производная.

Рассмотрим этот вопрос для первого интервала времени (от 0 до t₁). На этом интервале сигнал ошибки неизменный и равен напряжению пробоя стабилитрона. В пункте 4.1.1 получилась структурная модель, см. его (рис. 5, там сумматор, два воздействия и две передаточные функции).

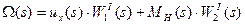
Когда производится включение, к системе ступенчато подводятся задающее напряжение и момент нагрузки (единичная ступенчатая функция). Это значит, что:

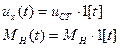
В процессе работы момент нагрузки неизменен, имеет определённое значение.

Изображения Лапласа этих сигналов:

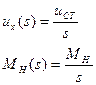
Передаточные функции:

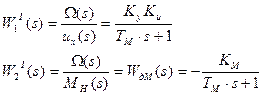
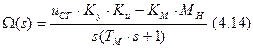
Остаётся воспользоваться таблицами соответствий (строка номер 5).

Для этого интервала времени получим:

????????

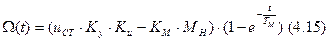
Нарисуем, какой вид будет иметь кривая переходного процесса на этом участке.

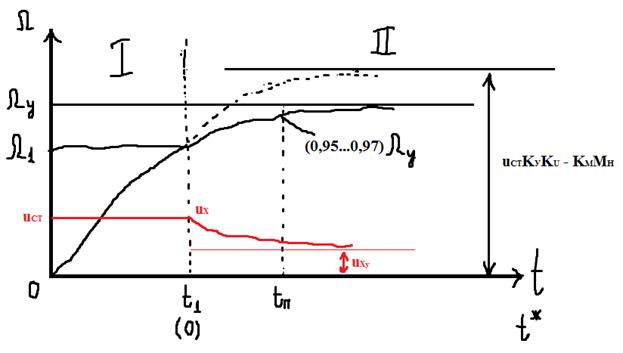
Начиная с момента времени t₁, вводится как бы «новое время» t^*, связанное с «реальным временем» через соотношение t^* = t-t₁. Для этого второго интервала будут наблюдаться ненулевые начальные условия, и Ω(t^*=0) = Ω₁. Теперь надо рассматривать передаточные функции Ф_З(s) и Ф_М(s).

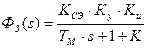
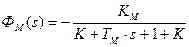
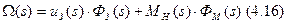
Так как опять рассматривается новое время с нуля, то в момент времени t^* происходит ступенчатое изменение входных воздействий – u_З(t) и M_Н(t).

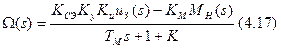
Эти передаточные функции выведены из предположения, что имеют место нулевые начальные условия. Тем не менее, уже эти передаточные функции позволяют найти дифференциальное уравнение всей системы.