Частотные характеристики дискретных элементов

При подаче на вход дискретного элемента решётчатого входного воздействия вида x[nT_д] = x_msin(ωnT_д), то на выходе получится гармоническая решётчатая функция (если подать на дискретный элемент; на непрерывном элементе на выходе получится непрерывная фунция, реакции на отдельные дельта-функции). Используя z-преобразование, можно найти выходные значения в дискретные моменты времени. Изобразим синусоиды после переходного процесса (в установившемся режиме).

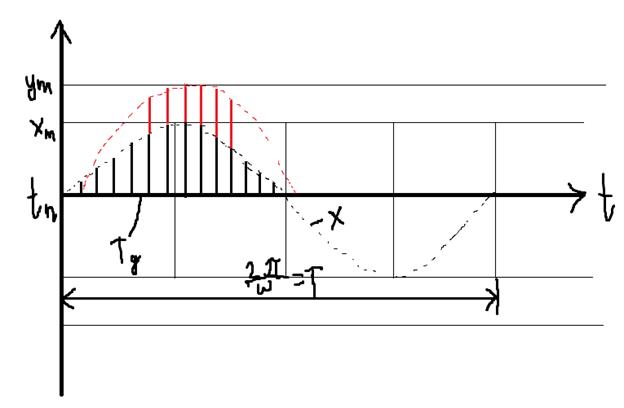
У выходного сигнала будет такая же частота, но будет наблюдаться фазовый сдвиг выходного колебания относительно входной решётчатой функции (ну и амплитуда, понятно). ВременнОе смещение будет равно:

Таким образом, для нахождения коэффициента передачи и фазового сдвига, надо располагать выражением для комплексного коэффициента передачи. Надо найти частотную передаточную функцию.

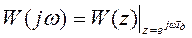
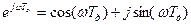
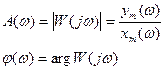
Пусть передаточная функция будет следующей:

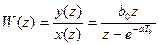
Найдём выражение для A(ω) и φ(ω).

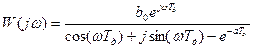
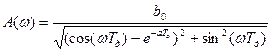
11.12.2012

Математические модели устройств радиоавтоматики, методы их анализа, синтез оптимальных структур