Передаточные функции дискретных систем радиоавтоматики
Для получения дискретной системы достаточно в непрерывную систему ввести идеальный импульсный элемент (ИИЭ). В этом случае структурная схема дискретной статической САР угловой скорости принимает следующий вид:
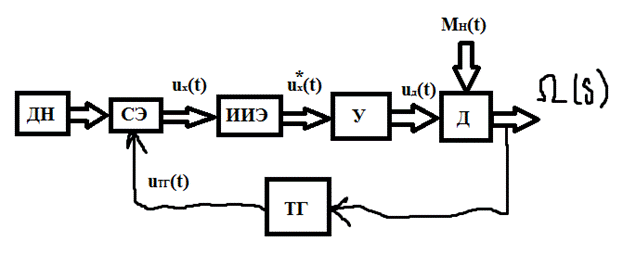
ux*(t) – обобщённая решётчатая функция, которая порождается сигналом ошибки ux(t).
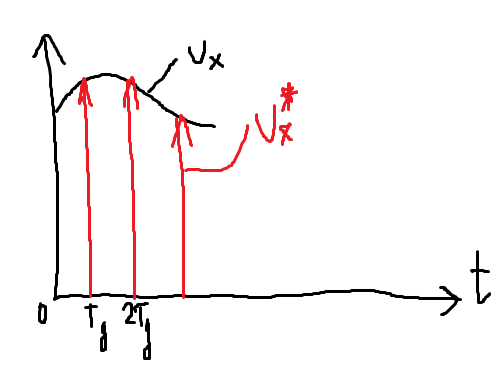
Линии со стрелочками – в дискретные моменты времени возникает на выходе дельта-функция, площадь которой равна ux[nTд].
Таким образом, обобщенная решётчатая функция – это совокупность дельта-функций, каждая из которых имеет свой вес (свою площадь). Математически это можно представить так:
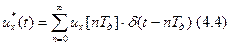
Таким образом, назначение идеального импульсного элемента – на короткое время соединять СЭ с усилителем. В этом случае будет проходить на вход усилителя мгновенное значение сигнала ошибки.
Изобразим структурную модель дискретной статической САР угловой скорости для динамического режима для интервала времени t1-Inf при условии, что МН = 0 (для упрощения).
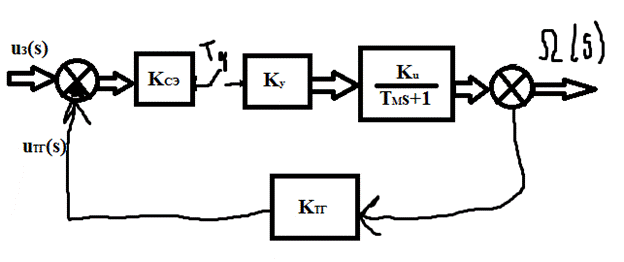
До ключа ux(s), после – ux*(s).
На практике это встречается редко. Чаще используют прямоугольные импульсы с достаточно длительным временем. Такие дискретные системы называют импульсными.
Преобразуем эту структурную модель, будет эквивалентное преобразование, которое не повлияет на расчёт Ω(s) и uТГ(s).
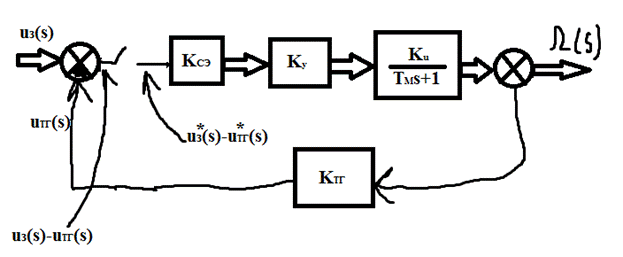
Очень важное значение для дискретных систем имеет значение передаточной функции разомкнутой САР, когда в качестве выходной величины рассматривается uТГ.
Найдём передаточную функцию непрерывной части разомкнутой дискретной САР:
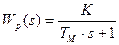
18.12.2012
Можно показать, что решётчатая функция на выходе тахогенератора можно представить следующим образом:
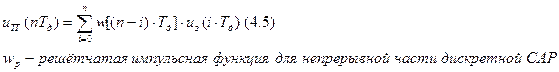
По теореме свёртки из выражения (4.5) вытекает, что z-преобразование напряжения на выходе тахогенератора равняется z-преобразованию от решётчатой импульсной функции (функции веса), перемноженному с uз(z):
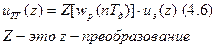
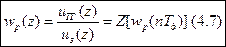
Надо найти импульсную функцию. Чтобы найти выражение для дискретной передаточной функции, надо знать решётчатую импульсную функцию wp(nTд). А она легко находится, если известно выражение Лапласа.
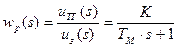
Надо поценить таблицы соответствий.
В итоге импульсная функция будет равна:
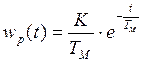
Дата добавления: 2020-10-25; просмотров: 530;











