А. Построение эпюр М и Q

Определяем реакции опор

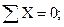Н_А = 0;

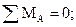
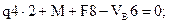
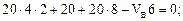V_B = 56,67 кН;

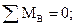
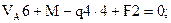
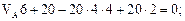
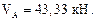
Проверка: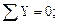

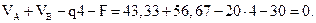
В отличие от предыдущего примера определим изгибающие моменты и поперечные силы в отдельных сечениях балки без составления функций для М и Q, используя только приведенные ранее (п. 7.1, стр. 122) рабочие правила и правила знаков.

Сечения проведем бесконечно близко в начале и в конце грузовых участков, на которых отсутствует распределенная нагрузка q. Дополнительное сечение проведем по середине участка, где имеется q (рис. 7.12 а).

Вычислим значения Q и М в этих сечениях. Для сечений 1–1, 2–2, 3–3 будем рассматривать левую отсеченную часть, а для остальных – правую часть.

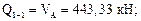
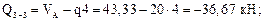
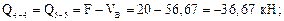
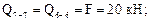
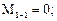
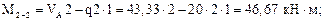
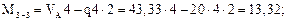
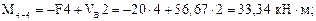
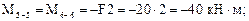
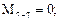
По полученным результатам строим эпюры М и Q (рис. 7.12б, в).

Эпюру М строим со стороны растянутых волокон, т.е. значения М со знаком "минус" откладываем вверх. Из эпюры Q видно, что экстремальное значение изгибающего момента на 1-м грузовом участке будет в сечении на расстоянии х₀, т.е. там, где Q(х₀) = 0. Из этого условия находим величину х₀:

Q(х₀) = V_A – qx₀ = 43,33 – 20x₀ = 0; x₀ =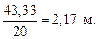

Вычисляем в этом сечении величину М_экстр:

М_экстр. = М(х = х₀) = 43,33 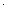2,17–20

При анализе правильности эпюр с учетом дифференциальных зависимостей между М, Q и q (7.13) замечаем:

– на эпюре М имеется скачок там, где приложен внешний сосредоточенный момент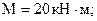

– на эпюре Q имеются скачки в сечениях, где приложены внешние сосредоточенные силы, в том числе и опорные реакции;

– на участках, где отсутствует q, эпюра моментов изменяется по линейному закону, а эпюра Q постоянна;

– на участке, где имеется равномерно распределенная нагрузка интенсивностью q, эпюра М меняется по закону квадратной параболы, выпуклостью в сторону действия q, а эпюра Q – по линейному закону. Тангенс угла наклона этой прямой к продольной оси балки равен интенсивности нагрузки q.