Передаточные функции непрерывных элементов

Для изучения и проектирования систем радиоавтоматики широко используют преобразование Лапласа реальных функций времени.

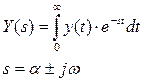
Зададимся y(t) = 1(t) – единичная ступенчатая функция.

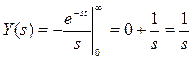
Математики составили таблицы, так что на практике выводить ничего не надо.

Y(s) – изображение по Лапласу. y(t) – это реальная функция времени (оригинал).

В результате преобразования Лапласа получается новая функция, которую называют изображением Лапласа. Реальную функцию времени можно зафиксировать для каждого момента времени, т.к. это реальная физическая величина, а изображение по Лапласу является не реальной функцией, и измерить её нельзя. Зато она позволяет решать многие практические задачи намного проще, чем с использованием только оригиналов. Это объясняется тем, что изображение выходной величины элемента можно найти простым перемножением изображения входной величины на передаточную функцию (в изображениях Лапласа) элемента.

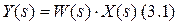
Если использовать функции времени, то для нахождения оригинала (y(t)) необходимо решать дифференциальное уравнение, что сложнее.

Из 3.1 вытекает определение передаточной функции элемента в изображениях Лапласа.

Передаточной функцией элемента в изображениях Лапласа с одним входом и с одним выходом называется отношение изображения выходной величины Y(s) к изображению входной величины X(s) при нулевых начальных условиях (выходная величина должна быть равна нулю).

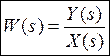
Для колебательного звена требуется, чтобы и в первых производных выходная величина была равна нулю.

Если элемент имеет два входа, тоже надо использовать (находить) две передаточные функции. Исходя из принципа суперпозиций, передаточная функция элемента по первому входному воздействию находится при X₂= 0.

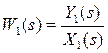
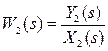
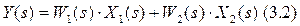
Выражение 3.2 позволяет построить структурную модель элемента для динамического режима.

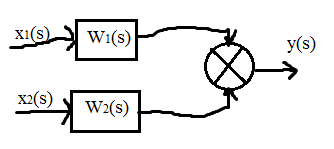
Тут уже не коэффициенты передачи для нулевой частоты (как в исследованиях САР в статическом режиме), а передаточные функции.

Передаточные функции можно легко найти, если известны математические модели элементов в виде алгебраических или дифференциальных линейных уравнений с постоянными коэффициентами. Найдём передаточные функции для коллекторного двигателя постоянного тока. Пусть это будет дифференциальное уравнение первого порядка.

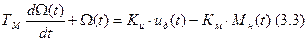
Т_м – электромеханическая постоянная времени.

u_д и М_н – входные величины. Выходная величина – Ω(t), угловая скорость. Значит, надо найти две передаточные функции – передаточная функция по напряжению и по моменту.

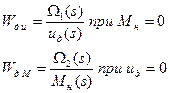
L – символ прямого преобразования Лапласа. L^-1 – символ обратного преобразования Лапласа.

Чтобы определить передаточные функции, надо левую и правую части преобразовать по Лапласу. При этом воспользуемся двумя свойствами преобразования Лапласа:

1) Свойство линейности.

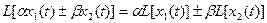
2) Изображение по Лапласу для первой производной равняется s. Но эта формула справедлива при нулевых начальных условиях.

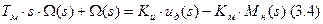
Теперь находим передаточные функции. Сначала по напряжению.

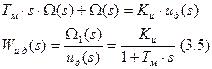
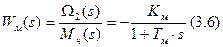
20.11.12

Так же легко найти передаточную функцию для дифференциального уравнения 2.1.

Решить дифференциальное уравнение – надо найти функцию(и) на всём промежутке времени работы изменение во времени выходной величины. При этом надо задаться характером изменения входных воздействий. Сие – анализ системы (параметры заданы, входные переменные заданы, задано устройство).

Если будем рассматривать уравнение 2.1, и в нём только одно воздействие x₁. Найдём передаточную функцию этого элемента по этому дифференциального уравнению.

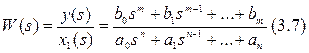
Для передаточной функции двигателя по напряжению – опять формула 3.5:

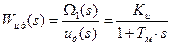
Таким образом: b_m = K_u; a_n = 1; a_n-1 = T_м.

Так как уравнение первого порядка, то в системе n = 1. Таким образом, а₁ = 1, а₀ = Т_м.

Зная передаточные функции двигателя в изображениях Лапласа, можно составить структурную модель двигателя для динамического режима.

Можно построить структурную модель двигателя для динамического режима (см. выше). В динамическом режиме выходная величина (входные величины тоже) изменяется во времени в установившемся режиме.

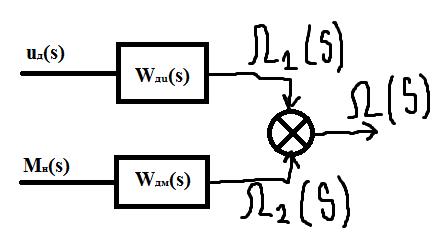
Чтобы найти изменение угловой скорости во времени, надо решать дифференциальное уравнение обыкновенное линейное первого порядка.

Если система нелинейная, то уже не получится такое упрощение, как принцип суперпозиций. Если, например, у коэффициента появится зависимость от времени, то при проведении операции перевода функции в изображение, получится большая суровость.

Математики нашли изображения большинства распространённых функций времени и составили обширные таблицы. Сделаем некоторые выдержки из этих таблиц.

№	Наименование функции	Оригинал f(t)	Изображение F(s)	z-изображение F(z)
	δ-функция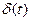
	Единичная ступенчатая	1[t]	1/s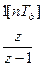
	Степенная	tn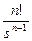
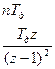
	Экспонента	e-at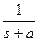
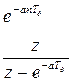
	Смещённая экспонента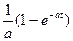
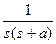
	Затухающая синусоида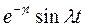
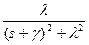
	Затухающая косинусоида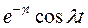
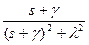
	Запаздывающая функция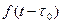

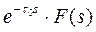
В выше перечисленных функциях подразумевается, что при t<0 функции равны нулю.

Исследователи и проектировщики широко используют эти таблицы. При этом избегают решения дифференциальных уравнений классическими методами для нахождения кривых переходных процессов. Очень прост метод построения кривых переходного процесса (изучение переходных процессов), базирующийся на изображениях Лапласа. Он включает в себя (на основании структурной модели):

1) Задание входной переменной (например, x₁(t)).

2) Нахождение изображений этих входных воздействий. Для этой цели используют эти таблицы.

3) Находится изображение выходной переменной (предполагается, что передаточные функции найдены).

4) Осуществляется обратное преобразование Лапласа (но опять же можно использовать таблицу).

Также кроме решения дифференциального уравнения, для определения характера изменения выходной величины можно применять интеграл Дюамеля (когда входная величина изменяется производная).