Математические модели линейных стационарных дискретных элементов
В дискретных системах наряду с непрерывными сигналами одновременно используются дискретные сигналы (входные и выходные дискретные величины). Дискретные сигналы делятся на:
- дискретизированные только по времени;
- дискретизированные одновременно по времени и по уровню;
- дискретизированные только по уровню.
Дискретизация по времени является линейной математической операцией, а квантование по уровню – нелинейной математической операцией. Но в данном разделе работа только с сигналами, дискретизированными по времени.
В математических моделях дискретных элементов рассматривают входные решётчатые функции и выходные решётчатые функции.
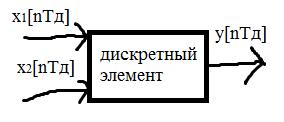
Тд – период дискретизации.
Тд = 1/fд.
n – номер текущего периода дискретизации.
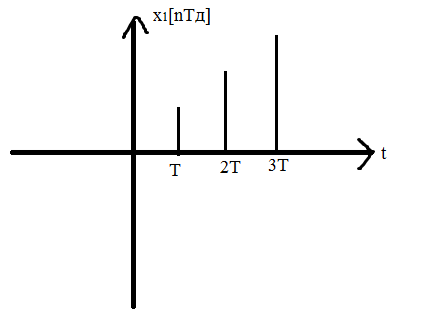
Если в системе появляется хотя бы один дискретный элемент, то она становится сразу дискретной.
Часто на входе дискретного элемента действуют непрерывные сигналы, и на входе происходит преобразование непрерывного сигнала в дискретизированный. В таком случае приходится говорить о преобразовании.
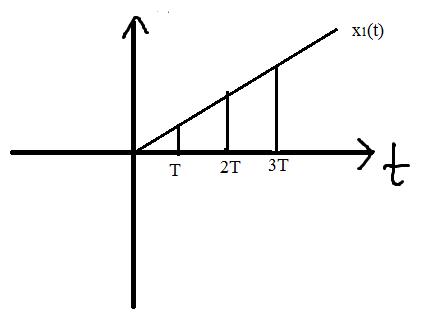

На практике это можно реализовать через электронный ключ.
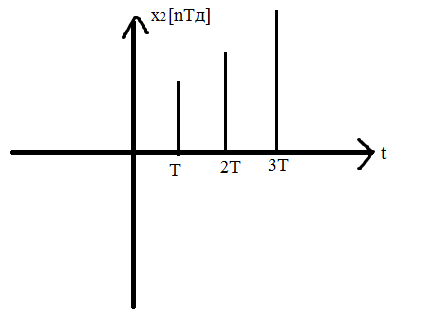
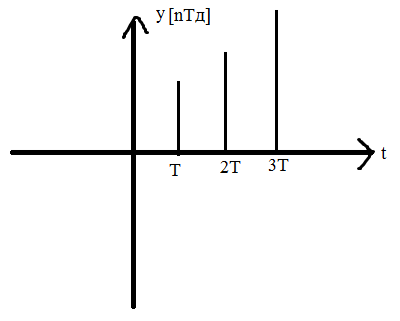
Для изучения переходных процессов дискретных линейных стационарных элементов используют линейные разностные уравнения с постоянными коэффициентами вида:
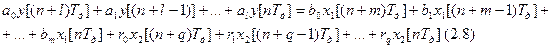
l – порядок элемента (а в непрерывных порядок элемента обозначался n). Например, l = 2, m = 1, q = 1. Тогда уравнение 2.8 преобразуется в следующее уравнение:
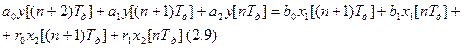
Пусть наступил статический режим. В этом случае y будет уже постоянным (а x1 и x2 уже постоянные). Найдём уравнение статики:
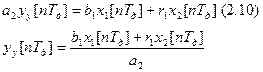
Дата добавления: 2020-10-25; просмотров: 515;











