Математические модели линейных стационарных непрерывных элементов

Классификация, данная для систем автоматики, справедлива и для линейных элементов.

Рассмотрим элемент с двумя входами и одним выходом. Два входа – две входные величины, выход – одна выходная. Это наиболее интересующие переменные, от них зависит выходная величина интересуемой функции. Чтобы изучить поведение системы в разных условиях, задаются разным характером изменений входных величин, изменяются параметры и так далее.

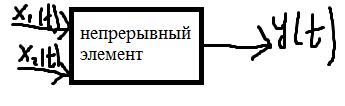
Для изучения переходных процессов непрерывных линейных элементов часто используются обыкновенные линейные дифференциальные уравнения с постоянными коэффициентами вида:

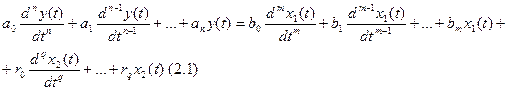
a, b, r – постоянные коэффициенты.

Система стационарная, т.к. в математической модели все коэффициенты являются постоянными. Если хотя бы один коэффициент будет зависеть от времени, то система станет нестационарной.

n – порядок элемента, порядок наивысшей производной, входящей в это дифференциальное уравнение. В реальных устройствах всегда выполняется условие, что m∙q ≤ n, в других случаях такой элемент будет нереализуем.

«Обыкновенное дифференциальное уравнение» – это значит, что тут нет частных производных.

m, q – порядки производных в правой части уравнения.

Уравнение 2.1 также служит основой для изучения поведения элемента в установившихся режимах. Математические модели для установившихся режимов намного проще, чем исходное уравнение для переходных процессов (это как бы объяснение «также»). Если установившийся режим является статическим, то из-за постоянства величин x₁, x₂ и y уравнение 2.1 преобразуется в уравнение статики вида:

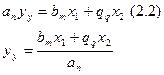
К входным величинам не надо приписывать индекс «у». Все величины не зависят от времени.

Если в установившемся режиме входные и выходные величины изменяются по гармоническому закону с одной частотой, то дифференцируя выходную величину (находя производные порядков n, n-1 и так далее), можно получить соотношение для расчёта амплитуды и фазы переменной y в установившемся режиме. В этом соотношении будут фигурировать соотношения для амплитуды и фазы входных величин.

Для линейных систем справедлив принцип суперпозиций: реакция системы на несколько одновременно приложенных воздействий равна сумме реакций системы на каждое воздействие в отдельности. В данном случае можно сначала рассмотреть реакцию на x₁ (x₂ приравнять к нулю), а потом реакцию на x₂ (x₁ приравнять к нулю), и потом суммировать.

Математическая модель системы, устройства, элемента иначе называют динамическим звеном. Для изучения и проектирования системы очень важно знать типовые динамические звенья, представляющие собой обыкновенные линейные дифференциальные уравнения с постоянными коэффициентами первого и второго порядка. Они с одной стороны просты, а с другой стороны позволяют математически описывать поведение многочисленных устройств различной физической природы. Всё это есть в литературе, также была лабораторная. К основным типовым динамическим звеньям относятся: