Функции затрат и их свойства

Рассмотрим функцию выпуска у =f(х) с одним продуктом и единственным ресурсом. Пусть эта функция - непрерывно дифференцируемая и удовлетворяет условиям:

f(0)=0; f’(x)>0 ,при х>0. (1)

В этом случае существует непрерывно дифференцируемая обратная функция: х = h(y). Это – функция затрат. В качестве примера функции f(х) можно рассмотреть функцию выпуска

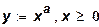
представленную в виде функции затрат

.

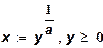Рассмотрим свойства функции затрат x = с(у). Из условия f(0)=0 следует, что

с(0) = 0, (2)

т. е. в случае отсутствия выпуска продукции тратить ресурс нет необходимости. Из условия f''(x)>0 ,при х>0 следует, что

c'(y) = l/f'(x)>0, (3)

это означает, что с ростом выпуска продукции затраты ресурса растут. Функцию c'(у)принято называть предельными затратами ресурсов. Как видно из (3), предельные затраты ресурса обратно пропорциональны предельной эффективности ресурсов.

Предположим, что для функции f(х) выполнено предположение об убывании предельной эффективности ресурса, т. е f''(х) <0. Тогда из (3) получаем, что функция с'(у)монотонно возрастает и

с"(у)>0. (4)

Введем понятие средних удельных затрат ресурса: g(y) = х/у. Отношение предельных затрат ресурса к средним удовлетворяет соотношению:

,

где а(х) - эластичность выпуска по ресурсу для f(х).

При выполнении предположения о том, что f''(х) <0, получаем, что а(х) < 1. Поэтому в таком случае предельные затраты ресурса больше средних. Для функции затрат х = y^l/a, порождаемой функцией выпуска .у = х^a, получаем:

; ,

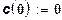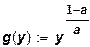c'(y) ,

с"(у) .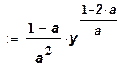

Графики перечисленных функций для функции затрат вида х = y^l/aпри а = 0,5 приведены на рис.1.

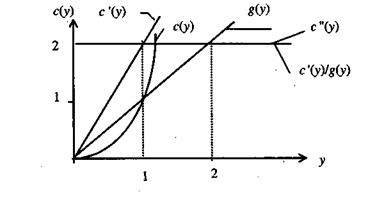
Рис.1.

Функция выпуска с одним продуктом и единственным ресурсом и соответствующая ей функция затрат эквивалентны: замена одной из них на другую не может привести к новым представлениям или дать преимущество при моделировании производственных единиц. Иное дело в случае нескольких ресурсов. Функция затрат для нескольких ресурсов и одного продукта имеет следующий вид:

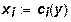, где i = 1,..., п.(5)

Потребление каждого из ресурсов задается однозначной функцией количества выпускаемой продукции. Замещение ресурсов здесь невозможно. Ресурсы в функции затрат являются взаимодополняющими, т. е. объемы потребления ресурсов определяются жесткими технологическими условиями, и нехватка хотя бы одного из ресурсов не позволяет полностью использовать остальные ресурсы. Таким образом, описание производства с помощью функции затрат принципиально отличается от описания с помощью функции выпуска, где замещение ресурсов допустимо.