Свойства степенной функции затрат в условиях совершенной конкуренции
Тем не менее, рассмотрение функций затрат позволяет вскрыть ряд интересных классических свойств.
Рассмотрим степенную производственную функцию с двумя ресурсами (х1 иx2) вида:
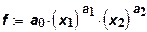
при этом затраты определяются как:
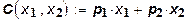 ,
,
и будем считать, что рынки ресурсов подчиняются законам совершенной конкуренции, так что цены 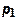 и
и 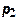 заданы для предприятия экзогенно.
заданы для предприятия экзогенно.
Для того чтобы определить функцию затрат, мы должны сначала отыскать комбинацию ресурсов, которые позволяют осуществить производство заданного количества 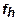 продукта с наименьшими затратами, т. е. максимизировать при быль при ограничении
продукта с наименьшими затратами, т. е. максимизировать при быль при ограничении 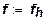 .
.
Применим метод Лагранжа. Функция Лагранжа будет иметь вид:
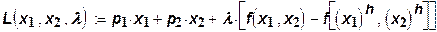
Возьмем первые производные и приравняем их к нулю:
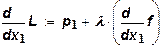
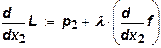
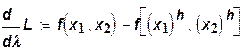
Из первых двух уравнений получаем, что предельные нормы замещения между ресурсами равны отношениям между ценами этих ресурсов:
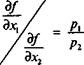
Предельные нормы замещения для данной производственной функции равны:
'
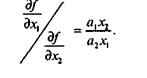
Откуда
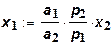
Тогда
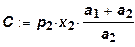 .
.
Из функции выпуска будем иметь:
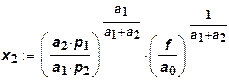
Теперь получаем окончательное выражение для функции затрат от выпуска:
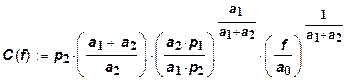
Предельные затраты будут равны:
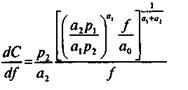
или после преобразований:
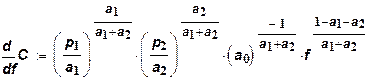
Если выразить прибыль как
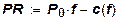 ,
,
то условием первого порядка нахождения максимума прибыли в условиях конкурентного равновесия будет равенство предельных затрат цене выпускаемой продукции:
Р0 = C'f.
Для выполнения условий второго порядка необходимо, чтобы вторая производная прибыли была отрицательная или равна нулю, т. е. чтобы предельные затраты были возрастающими или постоянными.
В точке равновесия множитель Лагранжа λ. равен предельным затратам.
Предположение о невозрастании предельной выручки влечет за собой постоянство или возрастание предельных затрат.
Кривая затрат, соответствующая производственной функции, предполагающей невозрастание предельной выработки, вогнута вверх. Классическая кривая, представляющая функцию затрат, вначале вогнута вниз. Эта часть кривой соответствует области значений выпуска, для которых неделимость играет существенную роль, а предельная выработка возрастает.
Заметим также, что предельные затраты постоянны, если производственная функция удовлетворяет гипотезе постоянства от изменения масштаба.
Функция предложения может быть получена приравниванием предельных затрат к цене продукта, что после преобразования дает:
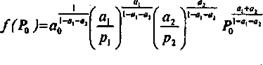
Дата добавления: 2020-10-25; просмотров: 454;











