Краткосрочные и долгосрочные решения
В некоторых случаях предприятие выбирает объемы использования не всех своих ресурсов, а только некоторых из них; использование других предопределено ранее. Таким образом, часто для одного и того же предприятия различают решения на длительный период, касающиеся всей организации производства, выбора оборудования и технологических процессов, а также решения на короткий период, касающиеся использования уже имеющихся в распоряжении производственных мощностей. Для решения на короткий период ресурсы задаются в соответствии с имеющимся оборудованием.
Рассмотрим вопрос на примере функции затрат, полученной из степенной производственной функции. Долгосрочную функцию затрат, в которой капитал также является переменной величиной, мы уже установили. Вид удельных средних и приростных затрат, т. е. на единицу выпуска, показан на рис. 5.
Рис. 5
Используя аналогичный метод, мы можем получить функции затрат для краткосрочных решений. В этом случае капитал будем рассматривать как постоянную величину. Тогда функция затрат для короткого периода из степенной производственной функции будет равна:
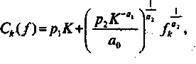 ,
,
где 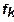 - соответствующая функция выпуска:
- соответствующая функция выпуска:
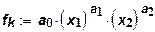 при
при 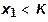 ;
;
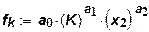 при
при 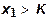 .
.
Характерный вид функций затрат приведен на рис. 6.

Рис.6
Предельные затраты для короткого периода будут равны:
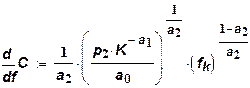
Вид предельных затрат представлен на рис. 7.

Рис.7
Предельные затраты на короткий период равны также равновесному значению множителя Лагранжа λ*.
Теория равновесия предприятия показана на рис.8, где представлены различные функции затрат как функции аргумента f.

Рис.8
Значение долгосрочного равновесия при цене продукции Р0определяется как абсцисса точки пересечения цены и функции предельных затрат долгосрочного периода. Значение равновесия на короткий период определяется как абсцисса точки пересечения функции предельных затрат на короткий период и цены продукции Р0.
Кривые долгосрочных и краткосрочных предельных затрат обычно имеют общую точку, соответствующую значению fh, для которой решение системы (14), определяющее долгосрочные затраты, дает для f значение fh,. В этой точки также удовлетворяются решения аналогичной системы для краткосрочных затрат. Поэтому в ней краткосрочные и долгосрочные предельные затраты равны, и они равны равновесному множителю Лагранжа. Также в этой точке кривые краткосрочных и долгосрочных средних затрат касаются друг друга. Этот результат может оказаться очевидным. Так как существующее оборудование совпадает с тем, которое предприятие выбирает на длительный период при тех же ценах, в этой точке долгосрочное и краткосрочное равновесие должны совпадать.
Кривая средних затрат за длительный период является огибающей кривых средних затрат за короткий период. Ни в каком случае краткосрочные затраты не могут быть меньше долгосрочных.
На практике получила большое распространение квадратичная регрессия, определяющая зависимость суммарных затрат, от объема выпуска:
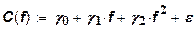
где 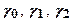 - параметры, устанавливаемые корреляционно-регрессионным анализом.
- параметры, устанавливаемые корреляционно-регрессионным анализом.
Дата добавления: 2020-10-25; просмотров: 491;











