Некоторые виды функций выпуска

Кроме перечисленных функций выпуска, существуют и другие функции. Наиболее распространенными являются линейная функция, функции Аллена, функции с линейной эластичностью замены факторов, функция Солоу, ограниченная функция CES, многорежимная функция, функция линейного программирования.

Линейная функция:

У данной функции предельные производительности факторов постоянны, эластичность замены факторов - бесконечна. Функция может использоваться в тех случаях, когда вклад каждого ресурса независим, например: производственная система состоит из отдельных производственных единиц, каждая из которых использует свой собственный производственный ресурс, подходящий только для этого производства.

Функция Аллена :

.

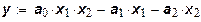Такая функция предназначена для описания производственных процессов, в которых чрезмерный рост любого из факторов оказывает отрицательное воздействие на объем выпуска. Обычно такая функция используется для описания мел­комасштабных систем с ограниченными возможностями переработки ресурсов.

Функция с линейной эластичностью замены факторов (функция LES):

.

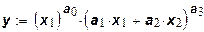Функция LES применяется для описания производственных процессов, у которых (в отличие от описываемых функцией CES) возможность замещения вовлекаемых факторов существенно зависит от их пропорций, причем при низком уровне отношений х₁/х₂близка к единице, а с ростом отношения х₁/х₂ - неограниченно возрастает. Такая ситуация возможна, например, если рост ресурсов х₁связан с общим расширением производства, появлением множественных технологических процессов с широкими возможностями комбинирования.

Функция Солоу:

.

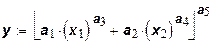Характеризуется тем, что величина процентного изменения предельной нормы замещения факторов, вызванного увеличением любого фактора на один процент, не зависит от начального уровня фактора. Эта функция может использоваться, когда влияние на объем выпуска увеличения каждого из факторов проявляется различным образом.

Ограниченная функция CES:

.

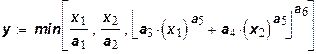Функция предназначена для выражения двухрежимного производственного процесса, в котором один из режимов характеризуется отсутствием заменяемости факторов, другой - ненулевой постоянной величиной эластичности замены При этом переход от одного режима к другому осуществляется в зависимости от уровня, лимитирующего первый режим фактора.

Многорежимная функция:

.

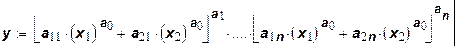Одна из наиболее общих форм производственных функций. Она используется при описании процессов, в которых уровень отдачи каждой новой единицы ресурса скачкообразно меняется в зависимости от соотношения факторов. Функцию целесообразно применять при наличии информации о числе режимов n и о ширине «переходной» области между режимами (чем выше а₀, тем более отчетливо выделяются режимы).

Функция линейного программирования:

.

Функцию имеет смысл использовать в тех случаях, когда выпуск продукции является результатом одновременного функционирования k-фиксированных технологий, использующих одни и те же ресурсы.