Производственные функции как основа описания закономерностей производства

Производственными функциями называют соотношения между используемыми в производстве материальными благами и трудовыми ресурсами (называемыми в совокупности производственными ресурсами), а также выпускаемой продукцией.

Пусть в модели рассматривается n производственных ресурсов. Количество i- го ресурса, используемого (или потребляемого) в течение некоторой единицы времени обозначим через x_i. Пусть выпускается тпродуктов, причем объем выпуска j-го продукта мы обозначим через y_j. Производственная функция связывает значение вектора продукции y со значениями вектора ресурсов х:

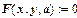(1)

где а = а₁,а₂,...,а_р- вектор параметров производственной функции.

Соотношение (1) может быть векторным, т. е. оно может состоять из не скольких равенств и может быть задано не только в аналитическом виде, но и виде таблицы.

Описание связи между использованием ресурсов и выпуском продукции виде (1) подразумевает, что не учитываются эффекты, связанные с продолжительностью производственного цикла, т. е. с периодом между затратами ресурсов и выпуском продукции. Далее в этой лекции будем предполагать, что это возможно в силу того, что единица времени, для которой строится производственная функция, значительно превосходит продолжительность производственного цикла.

Описание элементарной производственной единицы начинается с формулировки списка ресурсов и номенклатуры продукции с указанием характерных значений и пределов изменения этих величин.

Материальные производственные ресурсы необходимо различать по способам их расходования в производственных процессах. Обычно выделяют материальные ресурсы двух типов: предмет труда (сырье) и основные фонды (здания, оборудование и т. д.). Ресурсы первого типа в процессе производства в течении одного производственного цикла (периода выпуска продукции) расходуются полностью. Ресурсы второго типа используются в течение значительного числа производственных циклов.

Вместо общего представления производственных функций в виде (1) часто используют два частных случая.

1. Функция выпуска,в которой в качестве независимых переменных берутся затраты ресурсов, а функцией является выпуск:

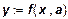. (2)

2. Функция производственных затрат,в которой независимой переменной является выпуск, а функцией - затраты:

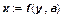. (3)

В соотношениях (2) и (3) величины х, у, и амогут быть многокомпонентными или векторными.

В том случае, когда вектор ресурсов х является многокомпонентным, между функциями выпуска и функциями затрат возникает принципиальное различие. В функции выпуска (2) возможны различные сочетания количеств производственных ресурсов, что приводит к тому, что один и тот же объем продукции может быть произведен при разных сочетаниях производственных ресурсов.

В функции затрат (3) задание выпуска продукции полностью определяет затраты ресурсов. Поэтому функция затрат используется в том случае, когда в описываемой элементарной экономической единице отсутствует возможность замещения одного ресурса другим.

Функция выпуска используется тогда, когда такая замена допустима. Как правило, в экономической литературе под производственной функцией подразумевают функцию выпуска.

С понятием производственной функции тесно связано понятие множество производственных возможностей,которое определяется как множество всех возможных сочетаний затрат трудовых материальных ресурсов и выпусков продукции:

[x,y] ÎG(a), (4)

где G(a) - некоторое множество G в пространстве ресурсов и продуктов, зависящее от вектора параметра (а).

Множество производственных возможностей задается соотношением:

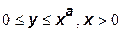, (5)

где а - параметр удовлетворяет соотношению .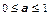

Множество производственных возможностей можно представить графически (рис. 1).

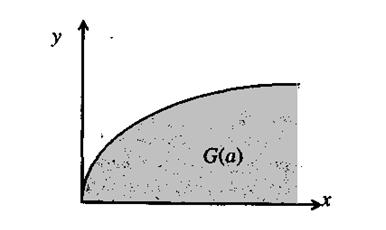
Рис.1

Связь между производственной функцией и множеством производственных возможностей устанавливается следующим образом. Предположим, что производство ведется эффективно, т. е. при данном количестве ресурсов выпускается максимально возможное количество продукции. Тогда имеет смысл рассматривать не все множество производственных возможностей, а только его границу:

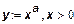(6)

Таким образом, мы получаем производственную функцию в виде функции выпуска. Если же с самого начала задана производственная функция в виде (6), то множество производственных возможностей можно получить, предполагая, что с помощью тех же ресурсов можно выпустить и меньшее количество продукции. Тогда из (6) с учетом того, что выпуск неотрицателен, сразу получается (5).

Аналогичным образом от описания множества производственных возможностей (5) можно перейти к функции затрат. Для этого необходимо предположить, что производство данного неотрицательного объема продукции у достигается при минимальных затратах ресурса х. Из (5) получаем функцию

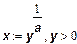, (7)

которая имеет вид функции затрат (3).

Заметим, что соотношения (6) и (7) описывают одну и ту же зависимость.

На рис. 2 изображены функция затрат (7) и множества производственных возможностей (5).

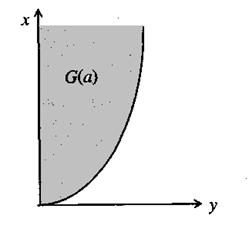Рис..2

Такая простая связь между множеством производственных возможностей производственными функциями устанавливается лишь в случае одного продукта и одного ресурса. В общем случае переход от множества производственных возможностей (4) к производственной функции (1) требует построения множества всех эффективных точек множества (4), т. е. всех таких объемов затрачиваемых ресурсов и выпускаемой продукции, что при данных затратах нельзя выпустить большее количество хотя бы одного вида продукции, не уменьшив производства других видов продукции. Кроме того, данного выпуска нельзя добиться при меньших затратах хотя 6ы одного ресурса, не увеличив при этом затраты других ресурсов.