Степенные производственные функции
 Степенная производственная функция с n ресурсами имеет следующий общий вид
Степенная производственная функция с n ресурсами имеет следующий общий вид
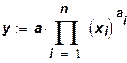
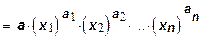 . {1)
. {1)
где у - объем продукции, который является скалярной величиной; а, а1, a2,... an - положительные параметры. Обычно предполагается, что ai < 1 для всех i = 1,…,n
Степенную производственную функцию (1) часто представляют в более удобном логарифмическом виде, эквивалентном (1) при xi > 0 (i = 1,…,n):
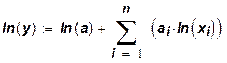
Степенные производственные функции были предложены в двадцатых годах двадцатого столетия Ч. Коббом и П. Дугласом для описания связи между объемом общественного продукта и двумя важнейшими ресурсами - трудовыми ресурсами и основными производственными фондами. В настоящее время степенные производственные функции используются для широкого класса экономических систем.
Для функции (1) выпуск продукции невозможен при отсутствии хотя бы одного ресурса.
Предельная эффективность j-го ресурса имеет вид:
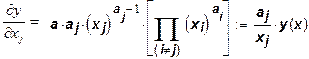 (2)
(2)
При xi > 0 (i = 1,…,n) имеем ¶y /¶xj> 0, причем в силу 0 < ai < 1 при стремлении xj к нулю предельная эффективность j-ro ресурса стремится к бесконечности, а при стремлении xj к бесконечности предельная эффективность стремится к нулю (конечно, при постоянных объемах других ресурсов).
Эластичность выпуска по j-му ресурсу легко получить из логарифмического представления степенной функции:
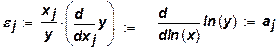 (3)
(3)
Соотношение (3) показывает роль параметров ai - это эластичность выпуска по соответствующему ресурсу. Учитывая экономический смысл эластичности выпуска по ресурсу, получаем, что показатели степени производственной функции (1) характеризуют отношение предельной и средней эффективностей использования производственных ресурсов. Таким образом, отношение этих двух эффективностей в степенной производственной функции не зависит от количества используемых ресурсов
Эластичность производства равна:

 . (4)
. (4)
В степенных производственных функциях выполняется предположение о наличии определенной отдачи от изменения масштабов производства. При Σai>1 имеем возрастающую, при Σai=1 - постоянную, а при Σ ai<1 – убывающую отдачу от увеличения масштабов производства.
Итак, степенная производственная функция удовлетворяет всем четырем предположениям о производственных функциях, сформулированных ранее.
Рассмотрим вопрос о замещаемости производственных ресурсов в степенной производственной функции (1). Предельные нормы замещения имеют вид:
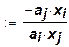
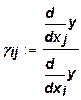 . (5)
. (5)
Предельные нормы замещения являются линейными функциями отношения объема ресурсов, поэтому изоклинали степенной производственной функции – плоскости (или линии при п = 2). При пропорциональном росте объемов производственных ресурсов предельная норма замещения не изменяется. При стремлении количества замещаемого ресурса к нулю предельная норма замещения падает, но остается положительной, т. е. возможность замещения сохраняется при любых малых (но не нулевых) количествах замещаемого ресурса.
Подсчитаем эластичность замещения 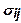 Прежде всего заметим, что из (5) следует:
Прежде всего заметим, что из (5) следует:
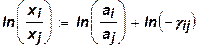
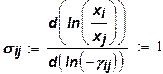 Поэтому:
Поэтому:
(6)
Таким образом, свойства производственной функции с двумя произволе венными ресурсами переносятся на степенные производственные функции с любым числом ресурсов. Равенство единице эластичности замещения ресурсов степенных производственных функциях вне зависимости от коэффициентов а, а1, a2,... an является одним из важнейших свойств производственных функций этого типа. Она показывает, что характеристика замещения одного ресурса другим при выборе степенной производственной функции задана заранее – вне зависимости от желания исследователя. Это является одним из недостатков степенной производственной функции вида (1).
Изокванты степенной производственной функции (1) описываются сое ношением:
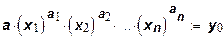
Для двух ресурсов характерный вид изоквант изображен на рис. 1. На рисунке изокванта приближается к оси координат при стремлении одного изресурсов к бесконечности. Это можно показать аналитически из уравнения изокванты:
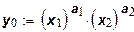
Получаем ее уравнение как функцию 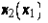 :
:
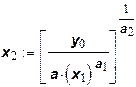 .
.
Отсюда в силу 0 < ai, <1 следует, что на изокванте 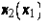
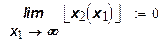
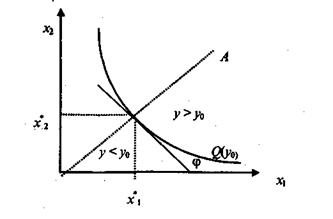 т. е. в соответствии с рис. 1 изокванта неограниченно приближается к оси x1. Аналогичным образом получаем, что при x2→∞ изокванта приближается к оси x2.
т. е. в соответствии с рис. 1 изокванта неограниченно приближается к оси x1. Аналогичным образом получаем, что при x2→∞ изокванта приближается к оси x2.
 Это стремление изоквант к координатным осям означает, что любое заранее заданное количество продукции может быть выпущено при сколь угодно малом количестве одного из ресурсов, если имеется в достаточном количестве другой ресурс. Такое свойство изоквант степенной ПФ с двумя ресурсами переносится на степенные ПФ с любым числом переменных (1): одним производственным ресурсом можно компенсировать недостаток всех остальных ресурсов.
Это стремление изоквант к координатным осям означает, что любое заранее заданное количество продукции может быть выпущено при сколь угодно малом количестве одного из ресурсов, если имеется в достаточном количестве другой ресурс. Такое свойство изоквант степенной ПФ с двумя ресурсами переносится на степенные ПФ с любым числом переменных (1): одним производственным ресурсом можно компенсировать недостаток всех остальных ресурсов.
Возможность замещения одного ресурса другим (равенство единице эластичности замещения ресурсов и неограниченная возможность компенсации недостатка одних ресурсов другими) часто вступает в противоречие со свойствами моделируемых производственных единиц. В связи с этим все чаще используются ПФ, близкие к степенной, но отличающиеся от нее возможностями замещения ресурсов. Такие функции характеризуются показателем эластичности замещения ресурсов, не равным единице.
Дата добавления: 2020-10-25; просмотров: 592;











