Свойства производственных функций

Обратимся к некоторым наиболее общим свойствам производственных функций, имеющих форму 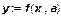, т. е. функций выпуска, допускающих замещение одного ресурса другим. Рассмотрим в данном разделе функции с одним продуктом и несколькими ресурсами – трудовыми и материальными.

Вектор параметров ав данном соотношении будем опускать, считая, что параметры уже определены и их влияние нас не интересует. Тогда функция выпуска приобретает вид:

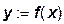, (8)

где: 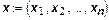- вектор.

Соотношение (8) задано при неотрицательных значениях компонентов вектора х.

Обычно относительно производственной функции (8) делают предположение, очень удобное с математической точки зрения, - о непрерывном изменении переменных х и достаточно плавном изменении выпуска при изменении затрат ресурсов. В математической форме эти предположения имеют следующий вид: функция (8) задана при всех неотрицательных значениях составляющих вектора хи является непрерывной или нужное число раз дифференцируемой функцией своих аргументов.

Перейдем к формулировке предположений (свойств), имеющих под собой экономическое обоснование. Для этого нам потребуются показатели предельного анализа.

Частная производная производственной функции по одному из ресурсов является предельной производительностью (эффективностью) данного ресурса - ¶f/¶x_i. Она характеризует скорость изменения функции выпуска по отношению к изменению затрат ресурса. Если предельная производительность ресурса положительна, то, следовательно, выпуск растет при росте затрат ресурса. Если предельная производительность ресурса отрицательна, то выпуск уменьшается при росте затрат ресурса.

Средней производительностью ресурса будет показатель f(x)/x_i.

Относительной характеристикой изменения выпуска продукции при увеличении затрат ресурсов будет показатель эластичности выпуска по отношению к изменению затрат i-го ресурса:

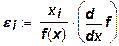
Эластичность выпуска по отношению к изменению затрат ресурса показывает, на сколько процентов возрастет объем продукции при увеличении затрат ресурсов на 1%.

Величину 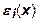можно вычислить по другой, эквивалентной формуле:

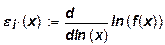
Определим данные показатели для производственной функции у = х^aпри х > 0. Предельная эффективность ресурса равна:

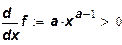
Средняя эффективность ресурса равна:

.

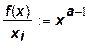В силу того, что 0 < а < 1, для этой производственной функции предельна эффективность меньше средней.

Эластичность выпуска по ресурсу будет равна:

=

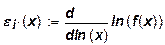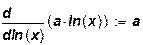
Эта производственная функция характеризуется постоянной эластичностью выпуска по отношению к изменению ресурса.

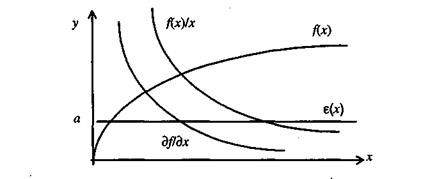
Рис. 3

На рис. 3 изображен график производственной функции 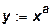, ее предельной и средней эффективностей, а также эластичности выпуска по ресурсу.

Теперь сформулируем экономические предположения.

Первое предположение. Производство невозможно при отсутствии хотя бы одного ресурса (точнее незаменимого ресурса), т. е.

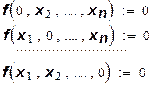; (5)

Это означает, что каждый из ресурсов необходим хотя бы в малых количествах. Полное его отсутствие не может быть компенсировано другими ресурсами.

Второе предположение. При увеличении затрат производственных ресурсов выпуск продукции не уменьшается. Это означает, что предельные эффективности ресурсов положительны. В математической форме:

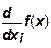≥0. (10)

Предположение (10), являющееся на первый взгляд очевидным, выполняется не всегда. Например, при возрастании количества удобрений, приходящихся на единицу площади, производство зерна сначала растет, а затем начинает снижаться. Поэтому для производственных функций, не удовлетворяющих соотношению (10), вводится понятие экономической области. Использование ресурсов в сочетаниях, не попадающих в экономическую область, бессмысленно с экономической точки зрения.

Для функций (8), имеющих непрерывные производные, границами экономической области являются поверхности ¶f/¶ х_i = 0, которые называют разделяющими поверхностями.

Третье предположение. По мере увеличения количества одного ресурса при постоянных количествах других предельная эффективность использования этого ресурса не возрастает. Математически это требование для дважды дифференци­руемых функций выглядит следующим образом:

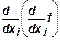≤0, 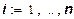. (11)

Для производственной функции вида 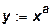это условие выполняется. Оно означает, что рост вооруженности средствами производства приводит к росту выпуска продукции, но темп роста выпуска продукции все время падает. В случае экстенсивного роста производства, т. е. роста только за счет количества ресурсов без повышения эффективности их использования на основе достижений научно-технического прогресса, соотношение (11) имеет разумную интерпретацию: поскольку каждая следующая единица производственного ресурса, количество которого возрастает, должна соединиться со все меньшим приходящимся на нее количеством других ресурсов, эффективность использования этого ресурса уменьшается.

Часто вместо условия (11) формулируется более сильное математическое требование, близкое к (11) по смыслу. Если f(x) – выпуклая вверх функция своих аргументов, на неотрицательном ортанте для любых двух неотрицательных векторов х' и х" и любого числа аÎ[0,1] справедливо неравенство:

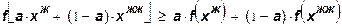. (12)

Если используется единственный ресурс, а функция f(x) достаточно гладкая то требования (11) и (12) равносильны. Если же ресурсов несколько то (11) не эквивалентно (12), т. е. не эквивалентно выпуклости вверх функции f(x).

Четвертое предположение. Производственная функция характеризуется определенной отдачей от расширения масштабов производства. Последняя характеризует изменение выпуска продукции при пропорциональном изменении затрат ресурсов и математически выражается в умножении всех компонентов вектора хна положительный скаляр t. Скалярная функция f(x) является однородной функцией степени δ, если для любого вектора хи любого скаляра tона удовлетворяет соотношению:

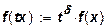. (13)

Математически четвертое предположение состоит в требовании однородности производственной функции. Если δ > 1, то производственная функция характеризуется возрастающей отдачей от расширения масштабов производства; если δ=1 – постоянной отдачей; при δ< 1 - убывающей отдачей. Естественно, что выполняется предположение δ ≥ 1, ибо в противном случае нарушалось бы условие (10) во всех точках положительного ортанта и отсутствовала бы экономическая область. Данное предположение выполняется далеко не для всех производственных функций, используемых в экономических исследованиях. Для характеристики последствий изменения масштаба производства вводят показатель ε(х), называемый эластичностью производства и определяемый следующие образом:

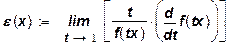(14)

Этот показатель характеризует процентное изменение выпуска продукции при изменении масштаба производства на 1% при данной структуре ресурсов х. Для производственных функций, удовлетворяющих соотношению (13), получаем .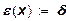

Можно установить связь между эластичностью производства и эластичностью выпуска по отношению к изменению затрат ресурсов ε_i(х). Учитывая, что

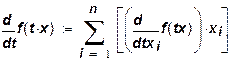, (15)

тогда

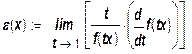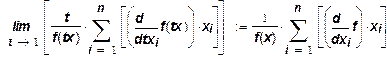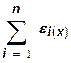= = (16)

Таким образом, эластичность производства в некоторой точке пространстве ресурсов равна сумме эластичности выпуска по отношению к затратам производственных ресурсов в этой точке.

В случае единственного ресурса, например в функции (6), эластичность производства совпадает с эластичностью выпуска по отношению к изменению затрат ресурса. Для производственных функций с постоянной отдачей от расширения масштабов производства (13) связь между эластичностями выпусков и эластичностью производства приобретает вид:

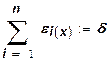. (17)

Рассмотрим производственные функции, удовлетворяющие четырем сформулированным выше предположениям, а именно: (9), (11). (13), (17). Возьмем t, удовлетворяющее условиям 0 < t < 1. Из условия (12) получаем:

.

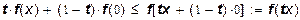Поскольку в силу (9) имеем 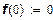, то 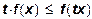. Из соотношения (13) получаем 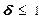, т. е. для выпуклых вверх производственных функций имеет место невозрастающая отдача от увеличения масштаба производства. Если производственная функция является строго выпуклой, условие (12) выполняется со знаком строгого неравенства (δ < 1). Это означает, что отдача от увеличения масштаба может быть только убывающей. Таким образом, для производственных функций, удовлетворяющих четырем соотношениям, в силу (17) и неотрицательности эластичности выпуска по ресурсам существует ограничение по эластичности выпуска:

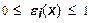. (18)

Таким образом, в основе производствен. функций лежат предположения, приведенные на рис.4.