Определение цен продуктов

Цены в системе межотраслевых связей определяются из системы уравнений, каждое из которых устанавливает, что цена единицы выпуска соответствующего производственного сектора должна быть равна совокупным издержкам в про­цессе производства этой продукции (в расчете на единицу выпуска). В эти из­держки входит не только оплата затрачиваемых ресурсов, но и добавленная стоимость, которая представляет собой в основном платежи секторам конечного спроса (d_i). Эти платежи состоят обычно из зарплаты, процента на капитал, предпринимательской прибыли, налогов, выплачиваемых правительству и дру­гим секторам конечного спроса.

Обозначим через p_i цену единицы i-го продукта. Тогда балансовые уравнения можно записать так:

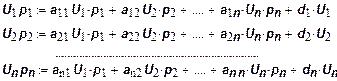
Сократив в обеих частях уравнений U_i получим систему уравнений:

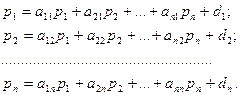
или в матричной форме:

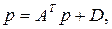
где А^T- транспонированная матрица технологических коэффициентов, а р и D - вектора цен и платежей секторам конечного спроса соответственно.

Матричное уравнение можно представить в виде:

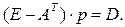
откуда получим в окончательном виде:

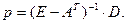
Данное уравнение позволяет определить соответствующую цену продукт отрасли. Элементы матрицы 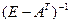измеряют зависимость цены р_j продукции сектора j добавленной стоимости d_i, полученной в секторе i в расчете на единицу продукции этого сектора.

В применявшемся выше примере добавленная стоимость, выплаченная в сельском хозяйстве и промышленности (т. е. зарплата), в расчете на единицу выпуска составляет 0,6 и 0,22 соответственно. Транспонированная матрица технологических коэффициентов равна:

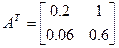
Далее рассчитываем:

,

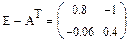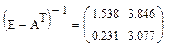
Тогда цены равны:

,

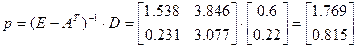т. е. цены на сельскохозяйственную и промышленную продукцию, используемые при расчете стоимостных показателей межотраслевых потоков.

Внутреннее единство стоимостных и физических взаимосвязей в рамках открытой системы межотраслевых связей подтверждается следующим тождеством:

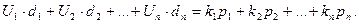
В левой части соотношения находится общая сумма добавленных стоимостей, выплаченная секторами системы секторам конечного спроса; в правой части - сумма стоимостей продуктов, доставленных всеми секторами секторам конечного спроса.

2. Разработка плана предприятия методом межотраслевого анализа

Метод межотраслевого анализа применим и для такой экономической системы, как предприятие. В этом случае место отраслей займут цеха, а конечного продукта - товарная продукция предприятия. Допустим, что предприятие состоит из ппроизводственных цехов, производящих однородные продукты 1, 2, ..., п. Основа технико-экономического плана промышленного предприятия есть система технико-экономических норм. В эту систему входят:

1. Нормы затрат .продуктов собственного производства в отдельных цехах; эти нормы можно представить в виде матрицы:

2. Нормы расхода сырья, основных материалов, топлива и электроэнергии на единицу продукта, произведенного в соответствующем цехе; эти нормы можно записать в виде матрицы:

.

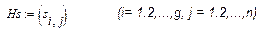3. Нормы времени работы машин и оборудования; эти нормы можно представить в виде матрицы:

.

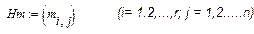4. Нормы, определяющие время работы отдельных групп персонала, необходимое для производства единицы продукта в соответствующем цехе; эти нормы можно представить в виде матрицы:

.

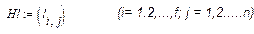Обозначим через U_i совокупную продукцию i-го цеха, а через k_i, - товарную продукцию этого цеха, т. е. ту часть совокупной продукции, которая остается после обеспечения производственных цехов и предназначается для сбыта. Поскольку затраты продукции i -го цеха на единицы продукта j-го цеха определяются по матрице 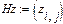,(i,j = 1,2,...,n) можно записать следующую систему уравнений:

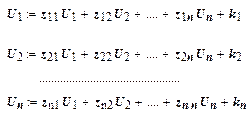
или в матричной форме:

U=HzU + K.

Решение, данного уравнения есть матрица:

U=(E - Hz)^-1 К.

Отсюда следует, что матрица продукции есть произведение матрицы норм полных затрат продуктов, произведенных отдельными цехами, и вектора плановой товарной продукции предприятия.

Матрица Hsнорм расхода сырья, материалов, топлива и электроэнергии есть основа плана материально - технического снабжения. Из матрицы Hsследует, что расходы отдельных видов сырья и материалов составляют:

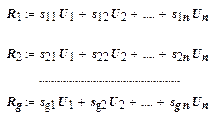
или в матричной форме:

R = HsU.

Подставляя выражение для определения матрицы товарной продукции, по­лучаем:

R = Hs(E-Hz)^-lK.

Элементы произведения Hs(E-Hz)^-lможно назвать коэффициентами полных затрат сырья и материалов. Матрицу потребности в сырье и материалах можно получить, умножив матрицу коэффициентов полных затрат сырья и материалов на вектор товарной продукции.

Матрица Нm - основа плана использования машин и оборудования. Использование машин и оборудования в производстве составляет:

,

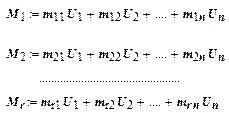или в матричной форме:

M = Нm U = Нm (E-Hz)^-1 К.

Элементы матрицы Нm (E-Hz)^-1называются коэффициентами полного иcпользования машин и оборудования. Матрицу плана использования машин оборудования можно получить, умножив матрицу коэффициентов полного иcпользования машин и оборудования на вектор товарной продукции.

Матрица hl- основа плана по труду. Матрица рабочей силы есть:

L = Hl.U = hl (E- Hz)^-1 К.

Элементы произведения hl (E- Hz)^-11 называются коэффициентами полных затрат рабочей силы. Матрица плановых затрат рабочей силы представляет собой произведение матрицы коэффициентов полных затрат рабочей силы и вектора товарной продукции.

Матричная форма технико-экономического плана в значительной мере упрощает планирование и уменьшает его трудоемкость: она позволяет быстро разработать различные варианты технико-экономического плана