Решение системы балансовых уравнений

Из определения технологических коэффициентов вытекает:

Следовательно, балансовые уравнения можно записать так:

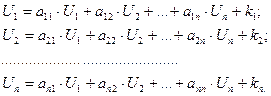
Или в матричной форме:

Введя обозначения:

получим матричное уравнение откуда:

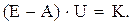
Умножим полученное уравнение на (Е-А)^-1:

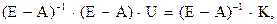
откуда:

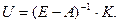
Планирование материального производства начинается с определения размеров и структуры общественного продукта. Решение матричного уравнения позволяет определить плановый объем производства отдельных продуктов таким образом, чтобы получить необходимые количества конечных продуктов. Полученное выражение позволяет быстро разработать разные варианты плана материального производства в соответствии с вариантами заданного конечного общественного продукта.

Введем обозначение:

Тогда можем записать:

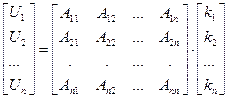
Умножив, получим:

Данное уравнение показывает, что элементы матрицы есть величины, определяющие количественные соотношения между конечными продуктами всех отраслей и продуктами каждой отрасли. Постоянные A_ij показывают, насколько увеличится выпуск U_i сектора i при увеличении k_j, т. е. количества товара j, потребляемого домашними хозяйствами (или любым другим потребителем этого сектора) на единицу.

В качестве примера рассмотрим нашу трехсекторную экономику, где матри­ца технологических коэффициентов равна:

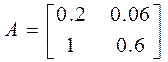
Примем два варианта потребности в конечном продукте:

1. k₁ = 50; k₂= 100,

2. k₁ = 75; k₂= 110.

Тогда

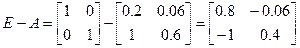
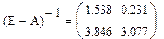
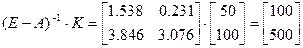
Для второго варианта имеем:

Кроме приведенной задачи, с помощью модели межотраслевого баланса ре­шаются и другие задачи: определение занятости в производстве; определение совокупных затрат труда; распределение совокупного общественного продукта; определение цен продуктов; определение размеров капитальных вложений. Рас­смотрим одну из них.