Особенности работы ЭВМ с числами с плавающей точкой.

Методы программирования на языке ФОРТРАН.

Сложные инженерные задачи (задачи сплошности) , использующие всё разнообразие численных методов программируют на языке ФОРТРАН. Данный язык наиболее универсален для сложных математических задач.

При решении сложных задач программа организуется на принципах структурного программирования, т.е. создаются некие структуры, организованные по общим принципам, обеспечивающим написание, отладку и запуск программы.

Главнейшее правило структурного программирования – модульность программ. Основным модулем (главным модулем программы) является модуль, организующий ввод начальных и исходных) данных и управление остальными модулями программы.

В задачах сплошности обязательно должен присутствовать модуль GEOM – геометрия рассчитываемого объекта.

Каждый модуль выполняет некий логически завершённый объём вычислений, при этом его вычисление могут быть основаны на результатах вычислений другого модуля, а его результаты, в свою очередь, передаются в третий и т.д.

При формировании тела модуля следует соблюдать некоторые правила составления и оформления:

1) первый оператор implicit none;

2) имя модуля носит смысловую нагрузку;

3) все переменные в теле модуля совпадают с физическими параметрами задачи;

4) имена переменных в модулях не менять;

5) при составлении тела модуля используются комментарии, дающие пояснения по входным и выходным параметрам модуля;

6) оформление тела модуля проводить в виде ступенек. Ступеньки должны показывать структурные участки внутри тела;

7) при написании тела модуля (изначально) присутствуют операторы промежуточной печати всех входных данных этой процедуры;

8) при написании тела модуля желательно соблюдать правило: если модуль превышает 200 операторов, то его следует разбить на подмодули;

9) при организации выдачи результатов работы программы выходные массивы числового материала следует формировать под соответствующие графические пакеты.

Особенности работы ЭВМ с числами с плавающей точкой.

Машинная числовая ось – конечное множество. При организации вычислений (арифметики) все компьютеры ориентированы на некую систему счисления. Большинство из них в независимости от системы счисления производят арифметические действия с числами с плавающей десятичной точкой. В компьютере число представляется в виде:

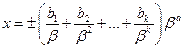
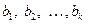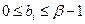
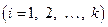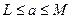где целые числа удовлетворяют неравенствам и . Если для каждого ненулевого 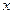из F справедливо , то система F называется нормализованной. Целое число 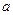называется показателем, а число 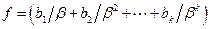- дробной частью. Обычно целое число 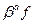хранится по той или иной схемам представления, принятым для целых чисел.

Пример. Перевод из двоичной системы счисления в десятичную систему.

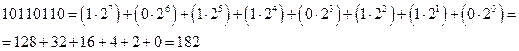
Пример. Перевод из десятичной системы счисления в двоичную систему.

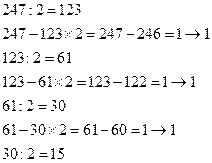
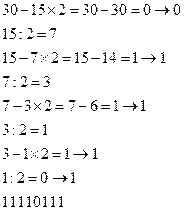
В силу ограниченности ячеек хранителей (памяти) для чисел компьютер в отличие от математической бесконечной числовой оси имеет некую числовую ось, на которой существуют две границы:

В отличие от математической числовой оси числовая ось компьютера «дырявая», т.е. на ней существует конечное число цифр, называемое множеством чисел машинной оси. Вышеназванные свойства числовой оси зависят от системы счисления компьютера 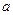и 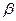. На разных компьютерах они различны.

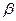
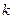
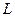
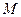
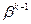
РДР-11			-128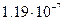
Сетунь			-121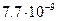
HP 45			-98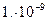
IBM 360/370			-64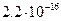

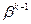- машинная точность (машинный эпсилон - ).

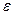Пример. Простейший компьютер организован со следующими параметрами:

,

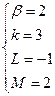
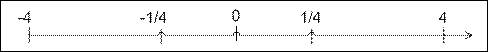
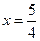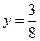
математическое: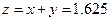

машинное: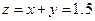

,

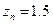При произведении вычислений на компьютерах различных фирм желательно оценить машинную ось данной ЭВМ. Для этого, пользуясь встроенными функциями фортрана найти Rmax, Rmin и найти машинный 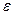данной ЭВМ. Под 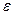понимают такое число, которое будучи добавленным к единице, эту единицу не меняет:

В зависимости от объявленной размерности переменной говорят о Rmax, Rmin с одинарной и двойной точностью.

По аналогии с вещественными числами вводится понятие Rmax, Rmin для целых чисел.

В силу особенностей машинной арифметики (конечности числовой оси) в процессе вычислений, особенно при циклических вычислениях, внутри компьютера нарастают ошибки, что может привести к абсолютно неверному результату. Существует большой пласт задач (динамика разреженного газа), где программист при составлении алгоритма вычислений должен предусмотреть накопление ошибки вычислений и разработать алгоритм вычислений, минимизирующий их.

В современном ФОРТРАНЕ в библиотеке IMSL есть встроенные функции, с помощью которых можно получить информацию о «машинной арифметике».

IMACH(I)

AMACH(I)

См. приложение 1 (Бартеньев. «Фортран для профессионалов. Математическая библиотека IMSL».)

Задание на лабораторную работу №1.

№1

Воспользовавшись функциями IMACH(I) и AMACH(I), выдать все параметры на печать. В ней же реализовать вычисления 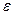по собственному алгоритму и сравнить с результатами, полученными с помощью AMACH.

№2

Оценить точность восстановления длины единичного отрезка в зависимости от числа его начального измельчения.

,

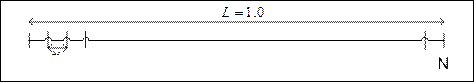
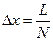№3

С помощью ряда для экспоненты рассчитать её значения для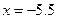

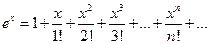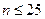, , результаты сравнить с результатом работы встроенной функции exp(x).