Долгосрочные издержки и расширение масштаба производства

Из представленных на рис. 2.4 графиков следует, что важнейшим фактором, определяющим конфигурацию кривой C_L(Q), является величина отдачи от масштаба производства, которая для производственной функции Кобба–Дугласа характеризуется значением показателя 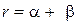. При постоянной отдаче от масштаба производства r=1 кривая C_L(Q) имеет вид луча, выходящего из начала координат. Это указывает на то, что долгосрочные издержки с расширением масштаба производства ( 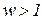) увеличиваются в той же пропорции, в какой растет объём выпуска Q.

Расширение масштаба производства связано с кратным увеличением используемых ресурсов. Поэтому

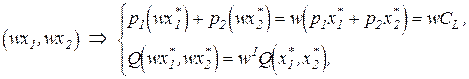
то есть как сумма затрат, так и объем выпуска продукции, возрастают в w раз.

При возрастающей отдаче r>1:

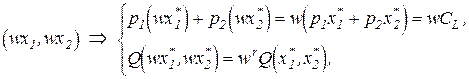
но 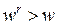, то есть рост объема выпуска опережает рост суммы издержек. Поэтому кривая C_L(Q) (рис. 2.4) выпукла вверх. Важно подчеркнуть, что издержки с увеличением объёма выпуска возрастают, но возрастают всё медленнее.

Наконец, на рис. 2.3 представлена кривая C_L(Q) для случая убывающей отдачи от масштаба производства r<1. В этом случае 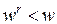, то есть при неизменных ценах затраты растут в большей степени, чем выпуск. Поэтому кривая C_L(Q) являетсявыпуклой вниз.

Долгосрочные средние издержки определяются как

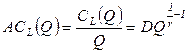. (2.8)

Долгосрочные предельные издержки определяются как

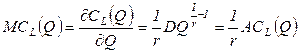. (2.9)

Из сравнения расчётных формул AC_L(Q) и MC_L(Q) следует, что конфигурация этих кривых совпадает, но их расположение друг относительно друга, благодаря значению множителя 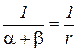, изменяется.

При постоянной отдаче 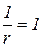, значит кривые AC_L(Q), MC_L(Q) совпадают. При возрастающей отдаче 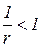, значит кривая MC_L(Q) будет располагаться ниже кривой средних затрат AC_L(Q). И, наконец, при убывающей отдаче 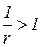, значит кривая MC_L(Q) пройдёт над кривой средних затрат AC_L(Q).

Пример 2.3.1. Для фирмы, рассмотренной в примере 2.2.1, построить и проанализировать графики AC_L(Q) и MC_L(Q).

Значения AC_L(Q) и MC_L(Q) рассчитаны по формулам (2.8), (2.9) и изображены на рис. 2.5, причем кривые средних издержек показаны сплошной линией, кривые предельных издержек - пунктирной линией. Увеличение объема выпуска при неизменной технологии обусловлено кратным множителю w увеличением используемых ресурсов. В случае постоянной отдачи от расширения масштаба производства (r=1) кривые средних и предельных издержек на рис. 2.5 совпадают. В случае возрастающей отдачи от расширения масштаба производства (r>1), кривые средних и предельных издержек будут убывающими, причем, поскольку предельные издержки отличаются от средних на множитель 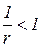, кривые будут сближаться. В случае убывающей отдачи от расширения масштаба производства (r<1) кривые средних и предельных издержек будут возрастающими и расходящимися, так как .

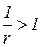По рис. можно определить, что при выпуске 4 тонн стекла в месяц фирма в среднем расходует 9 тыс. руб. на тонну (если эффект расширения масштаба положительный); при этом выпуск дополнительной (5-й) тонны стекла обойдется фирме в сумму 8 тыс. руб.

Таким образом, положительный эффект расширения масштаба производства заключается в том, что величины средних и предельных издержек снижаются с увеличением объема выпуска, причем уменьшение предельных издержек происходит опережающими темпами.

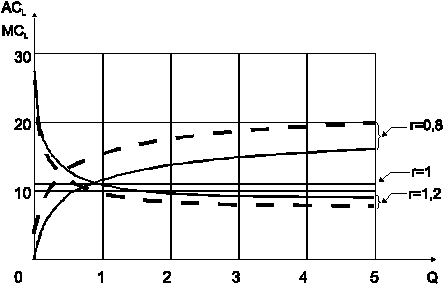
Рис. 2.5. Кривые долгосрочных средних и предельных издержек