Функция издержек в краткосрочном периоде
| Задача определения функции издержек |
Как отмечалось выше, в краткосрочном периоде количество некоторых ресурсов не может быть изменено. Будем полагать, что в двухфакторной модели количество второго ресурса неизменно и равно 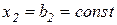 . Тогда задача минимизации краткосрочных издержек для фиксированного объема выпуска Q примет следующий вид:
. Тогда задача минимизации краткосрочных издержек для фиксированного объема выпуска Q примет следующий вид:
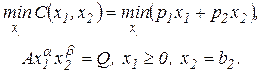
| Геометрическая интерпретация |
Эта задача также имеет наглядную геометрическую интерпретацию (рис. 2.6). Если перемещать изокосты по направлению к началу координат до тех пор, пока изокоста не пересечет изокванту, соответствующую выпуску Q, в точке ее пересечения с линией постоянного ресурса, то решением задачи минимизации издержек будет общая точка В с координатами 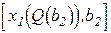 изокосты С2, фиксированной изокванты Q и линии постоянного ресурса.
изокосты С2, фиксированной изокванты Q и линии постоянного ресурса.
Долгосрочные издержки С3 при том же объеме выпуска Q определяются точкой касания изокосты С3 и фиксированной изокванты Q в точке А с координатами 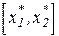 , причем величина долгосрочных издержек не превышает суммы краткосрочных издержек, так как изокоста С3 расположена не выше изокосты С2. Это означает, что затраты на выпуск одного и того же объема продукции в долгосрочном периоде не больше, чем в краткосрочном. Эти издержки производства могут быть равны друг другу, если
, причем величина долгосрочных издержек не превышает суммы краткосрочных издержек, так как изокоста С3 расположена не выше изокосты С2. Это означает, что затраты на выпуск одного и того же объема продукции в долгосрочном периоде не больше, чем в краткосрочном. Эти издержки производства могут быть равны друг другу, если 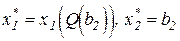 .
.
Увеличение располагаемого объема постоянного ресурса приводит к сдвигу линии постоянного ресурса вверх. В результате комбинация ресурсов, обеспечивающая объем выпуска Q, будет постепенно приближаться к точке с координатами 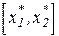 , то есть сумма издержек в долгосрочном периоде является пределом суммы издержек в краткосрочном периоде при стремлении запаса фиксированного ресурса к бесконечности (неограниченный располагаемый объем ресурса).
, то есть сумма издержек в долгосрочном периоде является пределом суммы издержек в краткосрочном периоде при стремлении запаса фиксированного ресурса к бесконечности (неограниченный располагаемый объем ресурса).

Рис. 2.6. Определение суммы издержек в краткосрочном периоде
| Аналитическое решение |
Для определения неизвестной х1 координаты точки В достаточно решить следующую систему уравнений:
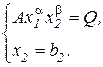
Первое уравнение системы характеризует фиксированную изокванту Q, а второе – линию постоянного ресурса. Очевидно, что искомая координата равна
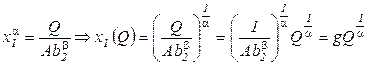 , (2.10)
, (2.10)
где 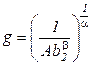 . Формула (2.10) позволяет рассчитать потребное количество переменного ресурса
. Формула (2.10) позволяет рассчитать потребное количество переменного ресурса 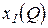 , обеспечивающее с постоянным ресурсом х2 выпуск Q. Причем количества ресурсов
, обеспечивающее с постоянным ресурсом х2 выпуск Q. Причем количества ресурсов 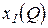 ,
, 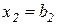 позволяют фирме осуществить выпуск Q при минимальных издержках, то есть являются функциями спроса на ресурсы. Определим эти издержки:
позволяют фирме осуществить выпуск Q при минимальных издержках, то есть являются функциями спроса на ресурсы. Определим эти издержки:
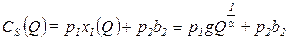 , (2.11)
, (2.11)
Первое слагаемое в функции краткосрочных издержек характеризует сумму переменных издержек, а второе слагаемое является вкладом фиксированных (постоянных) краткосрочных издержек.
Пример 2.4.1. Для стекольного завода, рассмотренного в примере 2.2.1, определить издержки в случае, если поставка топлива ограничена объемом 2 тонны в месяц при отсутствии эффекта расширения масштаба 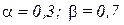 ; объем выпуска стекла составляет 4 тонны.
; объем выпуска стекла составляет 4 тонны.
Поскольку 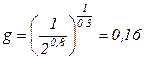 , то по формуле (2.11) рассчитаем
, то по формуле (2.11) рассчитаем 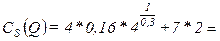 76 тыс. руб. Сравнив с результатом в примере 2.2.1, замечаем, что издержки в краткосрочном периоде, с учетом ограничения на поставку топлива, значительно возросли – на (76-45)=31 тыс. руб.
76 тыс. руб. Сравнив с результатом в примере 2.2.1, замечаем, что издержки в краткосрочном периоде, с учетом ограничения на поставку топлива, значительно возросли – на (76-45)=31 тыс. руб.
Дата добавления: 2020-10-25; просмотров: 609;











