Проблема рациональной коммерческой деятельности
| Функция коммерческой организации |
Коммерческая организация (предприятие, фирма) – это самостоятельно хозяйствующий субъект, созданный для производства продукции, выполнения работ или оказания услуг в целях удовлетворения общественной потребности и получения прибыли. В процессе коммерческой деятельности организация затрачивает экономические факторы (расходует приобретенные ресурсы) и реализует созданные товары (работы, услуги) другим хозяйствующим субъектам.
Перед организацией стоит задача выбора рационального (наивыгоднейшего) способа осуществления коммерческой деятельности. Условия задачи включают в себя:
§ вектор цен на факторы производства
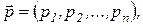
которые, как предполагается, определяются рыночным равновесием и не подвержены влиянию рассматриваемой организации;
§ номенклатуру ресурсов производства 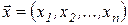 и вид производственной функции
и вид производственной функции 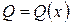 ;
;
§ уровень цены продукции фирмы 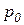 , определяемый рыночным равновесием;
, определяемый рыночным равновесием;
§ характеристики рынка, конкретизирующие предпосылки формирования цен на продукты и ресурсы:
· совершенная конкуренция при большом количестве взаимно независимых фирм, производящих стандартизированную продукцию, не оказывая влияния на ее цену;
· несовершенная конкуренция (монополистическая конкуренция, олигополия, монополия);
§ длительность периода:
· долгосрочный период, в течение которого организация имеет возможность выбрать любой неотрицательный вектор затрат

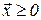 ;
;
· краткосрочный период, в рамках которого возможный выбор вектора затрат ограничен располагаемым запасом ресурсов
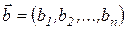 ,
,
то есть вектор затрат ограничен
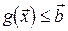 .
.
| Задача фирмы |
Основная задача коммерческой организации состоит в выборе: а) ассортимента и объема выпуска, то есть что производить и в каких количествах; б) производственной функции и суммы издержек, то есть каким технологическим способом и с какими затратами вести производство чтобы максимизировать прибыль.
Организация формирует финансовый результат (прибыль или убыток) продаж как разность периодического дохода R (Revenue) и издержек производства и реализации С (Costs):
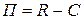 .
.
Доход за период вычисляется как произведение объема выпуска продукции на ее цену:
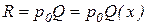 .
.
Издержки производства равны общим выплатам за приобретение всех ресурсов, использованных в производственном процессе:
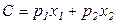 .
.
Фундаментальная задача фирмы заключается в выборе вектора ресурсов 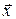 , максимизирующего прибыль организации:
, максимизирующего прибыль организации:
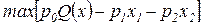 .
.
| Изопрофита |
Если зависимость суммы прибыли от объемов затрат факторов производства представлена в виде:
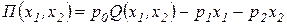 ,
,
то выразив из этого соотношения объем выпуска продукции
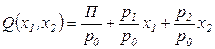 ,
,
получим зависимость объема выпуска Q от величин затраченных ресурсов при некотором значении прибыли П, которая называется изопрофитой (изопрофитной поверхностью). Если один из факторов (например, 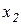 ) фиксирован, то изопрофита при постоянных ценах ресурсов представляет собой прямую линию с угловым коэффициентом, равным соотношению цен переменного фактора и продукта.
) фиксирован, то изопрофита при постоянных ценах ресурсов представляет собой прямую линию с угловым коэффициентом, равным соотношению цен переменного фактора и продукта.
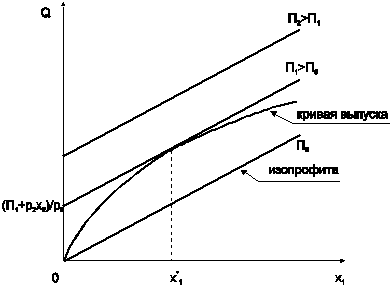
Рис. 3.1. Изопрофита
На рис. 3.1 показан вид изопрофиты при 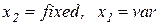 . Поскольку предельный продукт равен угловому коэффициенту касательной к кривой выпуска
. Поскольку предельный продукт равен угловому коэффициенту касательной к кривой выпуска
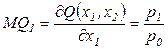 ,
,
то в некоторой точке изопрофита касается кривой выпуска. Абсцисса точки касания 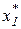 представляет собой оптимальный расход ресурса
представляет собой оптимальный расход ресурса 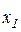 , обеспечивающий максимальную сумму прибыли при данном виде производственной функции.
, обеспечивающий максимальную сумму прибыли при данном виде производственной функции.
§3.2. Рациональная коммерческая деятельность
в условиях совершенной конкуренции
| Черты совершенной конкуренции |
Совершенная конкуренция как одна из моделей рынка имеет следующие особенности:
· наличие множества организаций, реализующих стандартизированные товары (услуги);
· доступ на рынок совершенно свободен, поэтому свободно перемещение ресурсов;
· объем продукции отдельной коммерческой организации несопоставим с объемом реализации данной продукции на рынке в целом по отрасли (Qфирмы<<Qотрасли), поэтому каждая организация продает продукцию по установившейся в рамках рыночного равновесия цене и не может оказывать на нее влияния.
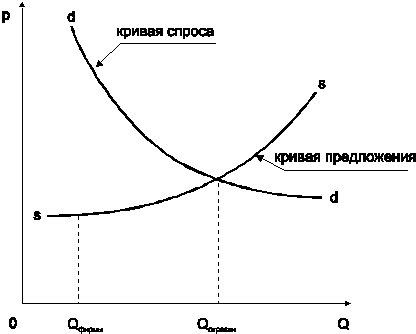
Рис. 3.2. Равновесие при совершенной конкуренции
В этих условиях функция предложения продукции данной организации (Qфирмы) на рис. 3.2 является кривой, приближающейся к горизонтальной прямой, то есть цена предложения не зависит от объема предложения организации.
Таким образом, условия совершенной конкуренции имеют вид:
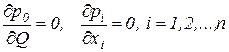 ,
,
где первое условие отражает конкуренцию на рынке товара, второе условие – конкуренцию на рынке ресурсов.
| Условия оптимальности в долгосрочном периоде |
Рассмотрим деятельность фирмы в долгосрочном периоде, то есть при неограниченных факторах производства. В условиях совершенной конкуренции основная задача коммерческой организации
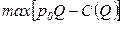
может быть решена в соответствии с необходимыми условиями экстремума функции одной переменной:
§ условие первого порядка
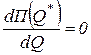 , (3.1)
, (3.1)
§ условие второго порядка
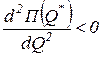 , (3.2)
, (3.2)
где Q* - оптимальное значение объема выпуска продукции.
Из условия первого порядка (3.1) следует, что
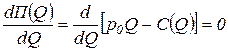 ,
,
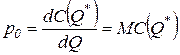 .
.
Поскольку цена предложения продукта представляет собой предельный доход MR, то есть прирост дохода организации в расчете на каждую дополнительную единицу продукции
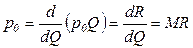 ,
,
то условие первого порядка приводит к необходимости равенства предельного дохода предельным издержкам при оптимальном объеме выпуска:
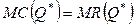 . (3.3)
. (3.3)
Условие второго порядка сводится к неравенству вида:
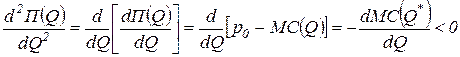 ,
,
или
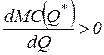 , (3.4)
, (3.4)
то есть при оптимальном объеме выпуска продукции предельные издержки должны возрастать.
| Геометрическая интерпретация |
Условие (3.3) выявляет две стационарные точки функции прибыли П(Q), в которых угол наклона касательной к кривой издержек С(Q) равен углу наклона прямой дохода – это точки с координатами Q’ и Q*, изображенные на рис. 3.3.
Однако точка Q’ принадлежит отрезку 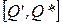 , на котором увеличение дохода превышает увеличение издержек, так как линия предельного дохода (прямая р0) лежит выше кривой предельных издержек. На отрезке
, на котором увеличение дохода превышает увеличение издержек, так как линия предельного дохода (прямая р0) лежит выше кривой предельных издержек. На отрезке 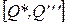 увеличение издержек превосходит увеличение дохода, поскольку кривая МС расположена выше линии р0. Условие (4) означает, что из точек Q’ и Q* нужно выбрать ту, которая соответствует восходящей ветви кривой МС.
увеличение издержек превосходит увеличение дохода, поскольку кривая МС расположена выше линии р0. Условие (4) означает, что из точек Q’ и Q* нужно выбрать ту, которая соответствует восходящей ветви кривой МС.
Таким образом, на участке 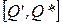 каждая дополнительная единица продукции увеличивает прибыль, а на участке отрезке
каждая дополнительная единица продукции увеличивает прибыль, а на участке отрезке 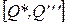 дополнительная единица выпуска уменьшает прибыль. Следовательно, для максимизации прибыли организация должна наращивать объем производства до тех пор, пока не будет достигнуто равенство цены продукции и предельных издержек при Q*, а затем прекратить наращивать объем выпуска.
дополнительная единица выпуска уменьшает прибыль. Следовательно, для максимизации прибыли организация должна наращивать объем производства до тех пор, пока не будет достигнуто равенство цены продукции и предельных издержек при Q*, а затем прекратить наращивать объем выпуска.
Кривая средних издержек АС является убывающей при АС>МС>0 и возрастающей при МС>АС>0; таким образом кривая средних издержек пересекает кривую предельных издержек в точке минимума средних издержек. Данная зависимость объясняется тем, что выпуск дополнительной единицы продукции, приводящей к приросту издержек на величину МС, меньшую среднего уровня издержек АС, снижает средние издержки; этот участок соответствует положительному эффекту расширения производства. Когда сумма издержек МС, обусловленная выпуском дополнительной единицы продукции, превышает установившийся в среднем по производству уровень издержек АС, то дальнейшее наращивание объема выпуска повышает величину средних издержек.
График средних издержек на рис. 3.3 пересекает линию р0 в точках Q” и Q’’’, характерных тем, что при таких объемах выпуска совокупные затраты С(Q) равны доходу 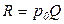 , то есть обеспечивается безубыточная деятельность. Отрезок bc характеризует прибыль, приходящуюся на единицу выпуска, так как bQ* - это доход с единицы продукции, а сQ* - издержки в расчете на единицу выпуска. Поэтому площадь прямоугольника abcd представляет собой совокупную прибыль организации.
, то есть обеспечивается безубыточная деятельность. Отрезок bc характеризует прибыль, приходящуюся на единицу выпуска, так как bQ* - это доход с единицы продукции, а сQ* - издержки в расчете на единицу выпуска. Поэтому площадь прямоугольника abcd представляет собой совокупную прибыль организации.
 |
Рис. 3.3. Оптимальный объем выпуска при совершенной конкуренции
| Обобщение условия MR=MC |
Условие равенства предельного дохода предельным издержкам
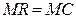
является ориентиром оптимальности выпуска с точки зрения прибыли и для других рыночных моделей, но только при совершенной конкуренции можно заменить предельный доход ценой, то есть условие
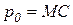
является частным случаем условия 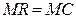 .
.
Планирование по конкурентной модели в долгосрочном периоде
| Особенности долгосрочного периода |
Рассмотренные в предыдущем параграфе необходимые условия оптимальности производственной программы получены без учета ограничений, накладываемых в связи с исчерпаемостью располагаемых объемов ресурсов. Таким образом, сформулированная модель представляет собой схему определения оптимального объема выпуска в долгосрочном периоде.
В долгосрочном периоде задача рациональной коммерческой деятельности является задачей безусловной оптимизации.
| Оптимальный план |
В качестве примера рассмотрим модель долгосрочного планирования
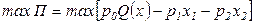
в случае двухфакторной производственной функции Кобба-Дугласа
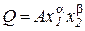 . (3.5)
. (3.5)
Условия оптимальности первого порядка позволяют определить объемы затрат каждого фактора, обеспечивающие максимальное значение прибыли:
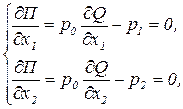

откуда следуют необходимые условия оптимальности:
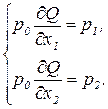
 (3.6)
(3.6)
Дифференцируя выражение производственной функции (3.5) и подставляя производные в (3.6), получим:
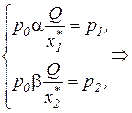
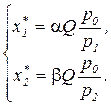 (3.7)
(3.7)
Это означает, что затраты ресурсов пропорциональны планируемому объему выпуска Q и обратно пропорциональны ценам, уплачиваемым при приобретении соответствующих ресурсов. Выражения (3.7) представляют собой функции спроса на ресурсы при совершенной конкуренции в долгосрочном периоде.
Из уравнений (3.7) вытекает, что
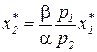 ,
,
то есть зависимость затрат одного ресурса от объема затрат другого является линейной функцией (рис. 3.5).
| Оптимальный объем выпуска |
Рассмотрим задачу определения объема выпуска продукции Q*, обеспечивающего максимальное значение прибыли в случае, если производственный процесс описывается функцией Кобба-Дугласа.
Подставим функции спроса (3.7) на факторы производства в функцию Кобба-Дугласа (3.6):
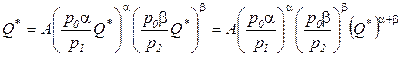 ,
,
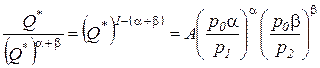 ,
,
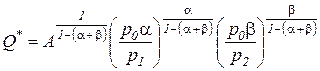 . (3.8)
. (3.8)
Таким образом, в случае положительного эффекта расширения масштаба производства ( 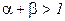 ) показатели степени
) показатели степени 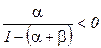 ,
, 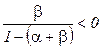 , следовательно оптимальное значение объема продукции тем больше, чем ниже цена продукта по сравнению с ценами ресурсов. При отрицательном эффекте расширения масштаба, имеющем более широкое распространение на практике, наблюдается обратная ситуация: чем значительнее цена продукта превосходит цены ресурсов, тем более высокого значения достигает оптимальный объем выпуска.
, следовательно оптимальное значение объема продукции тем больше, чем ниже цена продукта по сравнению с ценами ресурсов. При отрицательном эффекте расширения масштаба, имеющем более широкое распространение на практике, наблюдается обратная ситуация: чем значительнее цена продукта превосходит цены ресурсов, тем более высокого значения достигает оптимальный объем выпуска.
Пример 3.3.1. Для мукомольного завода, приобретающего зерно по цене 200 руб. за тонну и энергию по цене 300 руб. за килоВтчас, и реализующего муку по цене 10 тыс. руб. за тонну, определить оптимальный объем выпуска при различных типах эффекта расширения масштаба: а) возрастающая отдача от расширения масштаба 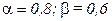 ; б) убывающая отдача от расширения масштаба
; б) убывающая отдача от расширения масштаба 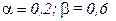 ; в) отсутствие эффекта расширения масштаба
; в) отсутствие эффекта расширения масштаба 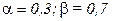 .
.
Рассчитаем оптимальный объем продукции по формуле (3.8) (в тоннах), полагая А=1.
а) 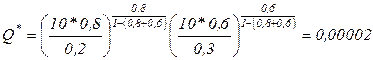 тонн, то есть при возрастающей отдаче от расширения производства (рис. 3.3) по формуле (3.8) определяется объем продукции Q’, при котором достигается наименьшая прибыль фирмы (зона убытка); дальнейшее расширение производства в этом случае приведет к увеличению прибыли – в данной ситуации расчета оптимального объема производства не требуется, так как фирме выгодно бесконечно расширять производство;
тонн, то есть при возрастающей отдаче от расширения производства (рис. 3.3) по формуле (3.8) определяется объем продукции Q’, при котором достигается наименьшая прибыль фирмы (зона убытка); дальнейшее расширение производства в этом случае приведет к увеличению прибыли – в данной ситуации расчета оптимального объема производства не требуется, так как фирме выгодно бесконечно расширять производство;
б) 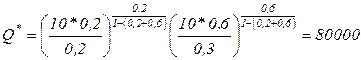 тонн; при убывающей отдаче от расширения производства (рис. 3.3) увеличение объема выпуска свыше 80 тыс. тонн в год невыгодно фирме, так как прибыль будет снижаться;
тонн; при убывающей отдаче от расширения производства (рис. 3.3) увеличение объема выпуска свыше 80 тыс. тонн в год невыгодно фирме, так как прибыль будет снижаться;
в) при a+b=1 применения формулы (3.8) не требуется; достаточно рассчитать предельные издержки, которые в этом случае постоянны и равны средним издержкам (формула (2.8)):
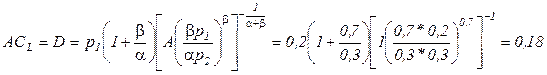 тыс. руб.;
тыс. руб.;
поскольку цена продукции 10 тыс. руб. превышает среднюю себестоимость продукции (180 руб. за тонну), то в этом случае фирме выгодно неограниченно наращивать производство; если бы средние издержки были выше цены продукции, то производство необходимо было бы прекратить. Подробнее данная методика анализа будет рассмотрена в §3.5.
| Кривая предложения фирмы |
Полученное выражение наивыгоднейшего объема выпуска продукции как функции цены продукции и цен ресурсов носит название функции предложения фирмы с производственной функцией Кобба-Дугласа:
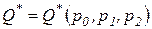 .
.
Эту функцию можно использовать для построения кривой предложения, показывающей зависимость цены предложения от объема предложения фирмы:
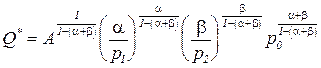 Þ
Þ 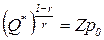 ,
,
где 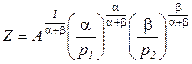 – постоянная величина, не зависящая от цены продукта;
– постоянная величина, не зависящая от цены продукта; 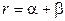 – степень однородности производственной функции. Поэтому
– степень однородности производственной функции. Поэтому
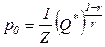 .
.
На рис. 3.4 изображены кривые предложения для случаев: а) постоянной отдачи от расширения масштаба производства (r=1), 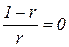 ; б) возрастающей отдачи
; б) возрастающей отдачи 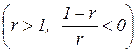 ; в) убывающей отдачи
; в) убывающей отдачи 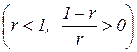 .
.
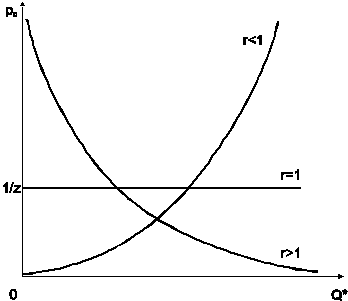
Рис. 3.4. Кривые предложения фирмы
Таким образом, в случае возрастающей отдачи от расширения производства, когда издержки фирмы растут замедленными темпами по сравнению с ростом производства, то есть средняя себестоимость продукции снижается, фирма имеет возможность продавать больший объем продукции по пониженной цене, продолжая получать максимальную прибыль. Эта ситуация позволяет фирме следовать стратегии освоения («захвата») рынка сбыта.
Постоянная отдача от расширения производства выражается в том, что средняя себестоимость продукции не изменяется, что дает возможность фирме сохранять цену продукции неизменной. Такая ситуация характерна для стратегии стабильного развития фирмы, функционирующей в режиме плановой загрузки.
Убывающая отдача от расширения производства, связанная с ростом средней себестоимости продукции, обусловливает необходимость повышения цены при увеличении предложения продукции с целью сохранения максимальной прибыли. Это приводит к падению конкурентоспособности продукции и сужает рынок сбыта.
Планирование по конкурентной модели в краткосрочном периоде
| Особенности краткосрочного периода |
В рамках краткосрочного периода ограничение на ресурсы приводит к ограничению на объем выпуска 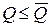 , и соответствующему ограничению величины прибыли, которая может в данном случае не достигать оптимального значения; в этом случае
, и соответствующему ограничению величины прибыли, которая может в данном случае не достигать оптимального значения; в этом случае
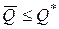 ,
,
и значение 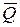 , определяемое ограничением
, определяемое ограничением 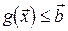 (как правило, при обращении нестрогого неравенства в равенство), следует рассматривать как оптимальный объем выпуска в краткосрочном периоде.
(как правило, при обращении нестрогого неравенства в равенство), следует рассматривать как оптимальный объем выпуска в краткосрочном периоде.
Таким образом, если в долгосрочном периоде задача рациональной коммерческой деятельности формулировалась как задача безусловной оптимизации, то при краткосрочном планировании возникает задача на определение условного экстремума.
| Оптимальный план |
При краткосрочном планировании предположим, что первый ресурс ограничен величиной запаса b1, а второй имеется в неограниченном количестве.
В этом случае формируется функция Лагранжа, которая в случае двух факторов и одного ограничения имеет вид:
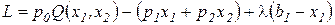 ,
,
и необходимые условия оптимальности записываются следующим образом:
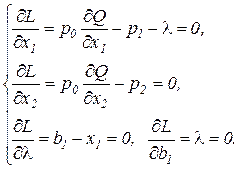
С учетом вида производственной функции Кобба-Дугласа из необходимых условий оптимальности следует:
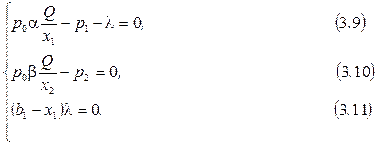
Выражения (3.9)-(3.11) являются объединением условий
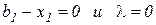 ,
,
поскольку они не могут выполняться совместно:
· если 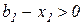 , то есть
, то есть 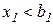 , то множитель Лагранжа
, то множитель Лагранжа  показывает величину прироста дохода, который можно получить с единицы неиспользованного резерва ресурса
показывает величину прироста дохода, который можно получить с единицы неиспользованного резерва ресурса 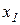 ; следовательно
; следовательно 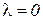 ;
;
· если 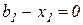 , то есть ресурс
, то есть ресурс 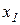 использован в полном объеме, то значение
использован в полном объеме, то значение  может быть любым
может быть любым 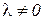 ;
;
· если 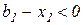 , то есть
, то есть 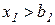 , то множитель Лагранжа
, то множитель Лагранжа  представляет собой сумму снижения дохода с единицы превышения запаса ресурса, а так как превышение считается невозможным, то
представляет собой сумму снижения дохода с единицы превышения запаса ресурса, а так как превышение считается невозможным, то 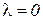 .
.
Таким образом, при краткосрочном планировании возможны два случая:
§ Изменение объема выпуска до некоторой величины, ограниченной условием 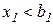 , то есть из уравнения (3.9) при
, то есть из уравнения (3.9) при 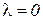 и х1=b1,:
и х1=b1,:
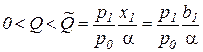 ;
;
в этом случае оптимальные значения факторов рассчитываются так же, как в долгосрочном периоде (так как 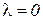 ):
):
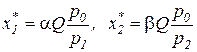 .
.
§ Более значительное изменение объема выпуска, соответствующее полному исчерпанию ограниченного ресурса; в этом случае оптимальные значения равны:
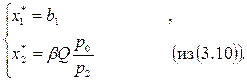 (3.12)
(3.12)
Характерно, что при увеличении значения фиксированного ресурса ( 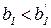 ) изменяется объем выпуска, соответствующий границе между долгосрочным и краткосрочным планами. Геометрическая интерпретация решения приведена на рис. 3.5.
) изменяется объем выпуска, соответствующий границе между долгосрочным и краткосрочным планами. Геометрическая интерпретация решения приведена на рис. 3.5.
 |
Рис. 3.5. Долгосрочны и краткосрочный планы
Объем затрат второго ресурса для оптимального плана определяется из соотношения (3.12) с учетом вида производственной функции:
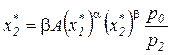 , Þ
, Þ 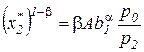 ,
,
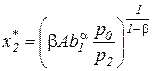 . (3.13)
. (3.13)
Поскольку показатель степени 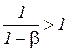 , то величина затрат второго (переменного) ресурса возрастает нелинейно при увеличении соотношения цен
, то величина затрат второго (переменного) ресурса возрастает нелинейно при увеличении соотношения цен 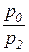 , то есть чем дешевле изменяемый ресурс, тем в большем объеме он будет расходоваться для обеспечения оптимального значения объема выпуска. Кроме того, большему значению
, то есть чем дешевле изменяемый ресурс, тем в большем объеме он будет расходоваться для обеспечения оптимального значения объема выпуска. Кроме того, большему значению 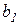 ограниченного ресурса соответствуют более значительные затраты переменного ресурса (при
ограниченного ресурса соответствуют более значительные затраты переменного ресурса (при 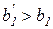 на рис. 3.5).
на рис. 3.5).
| Оптимальный объем выпуска |
Оптимальный объем выпущенной продукции определяется из выражения производственной функции Кобба-Дугласа с учетом соотношения (3.12):
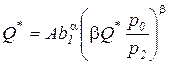 ,
,
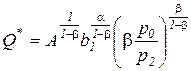 . (3.14)
. (3.14)
Поскольку в реальных производственных процессах, как было показано в работах Д. Кобба и П. Дугласа, значения показателей эластичности равны a=0,25, b=0,75, то из выражения (3.14) следуют выводы:
· оптимальный объем продукции возрастает пропорционально увеличению запаса фиксированного ресурса, так как 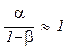 ;
;
· оптимальный объем выпуска возрастает ускоренными темпами с увеличением соотношения цен продукта и переменного ресурса, так как 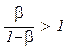 ;
;
· значение оптимального объема выпуска не зависит от цены фиксированного ресурса.
Пример 3.4.1. Решить пример 3.3.1, если поставки зерна ограничены объемом 400 тонн в год. а) 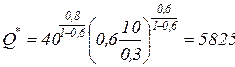 тыс. тонн; б)
тыс. тонн; б) 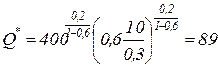 тонн; в)
тонн; в) 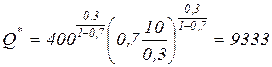 тонн;
тонн;
Во всех случаях оптимальный объем выпуска снизился.
Дата добавления: 2020-10-25; просмотров: 615;











