Оценка равенства дисперсий

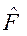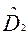Опенки гипотезы Н_о: D₁=D₂ производятся по критерию Фишера (6.34). Если значение >F _α, определенного по таб­лице при данном уровне значимости и числах степеней свободы υ ₁= n₁—1 и υ ₂ = n₂—1, то расхождение между и можно считать существенным и, следовательно, гипотезу о том, что вы­борки взяты из нормальных общих совокупностей с одинаковой дисперсией опровергнутой. Если же 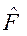< F _α, , то расхождение не существенно и гипотеза о равенстве дисперсий не опровергается.

В некоторых случаях для оценки равенства дисперсий исполь­зуется критерий Романовского.. Расчет производится в следующей последовательности.

Сначала рассчитывается вспомогательная величина :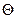

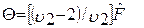, (6.43)

где 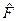— дисперсионное отношение, v₂ — число степеней свободы больше 4.

Математическое ожидание 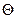для выборок из нормальной сово­купности с одинаковой дисперсией равно единице, т. е.

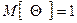, (6.44)

а среднее квадратическое отклонение

.

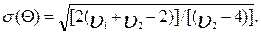(6.46)

С вероятностью р 0,99 можно ожидать, что абсолютная ве­личина отклонения 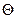от 1 по модулю не превышает З 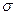. Отсюда следует, что, если выборки относятся к одной генеральной совокупности, то

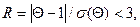
(6.47)

т. е. расхождение выборочных оценок дисперсий несущественно. Если R 3, то расхождение существенно.