Оценка среднего значения
Оценка среднего значения производится при помощи статистики t, являющейся нормированным отклонением выборочного среднего значения , от математического ожидания
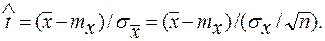 (6.20)
(6.20)
Математическое ожидание статистики t и ее среднее квадратическое отклонение равны соответственно 0 и 1 (см. разд. 3.1.3). Распределение статистики t подчиняется при некоторых условиях закону t-распределения Стьюдента.
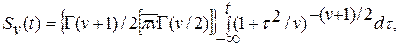 (6.21)
(6.21)
где v — число степеней свободы
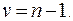 (6.22)
(6.22)
Формула (6.21) выражает вероятность случайных значений τ меньших, чем заданные значения t, т. е.
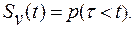 (6.23)
(6.23)
Указанное соотношение может быть использовано для определения значимости или существенности расхождения между выборочным и предполагаемым генеральным значением параметра распределения а, или между действительными значениями параметра а по разным выборкам. Так, если вероятность данного расхождения выборочной характеристики с генеральной составляет менее 1-5 %, т. е. очень мало, то, по-видимому, расхождение существенно или значимо. Обычно вопрос о значимости решается с помощью таблицы значений t, соответствующих данному уровню значимости а при данном числе степеней свободы v (см., например, работу [63], прилож. 7). В заголовке таблицы в первой строке указаны уровни значимости при использовании одностороннего критерия значимости (см. разд. 6.3), когда необходимо знать вероятность того, что t превосходит некоторое значение только в положительном (или только в отрицательном) направлении, а во второй строке указаны уровни значимости при использовании двухстороннего критерия значимости, когда определяется вероятность того, что t будет по абсолютной величине больше некоторого значения.
При малых значениях степеней свободы t-распределение Стьюдента заметно отличается от нормального распределения[A1] (рис. 6.3). Основное различие заключается в том, что для формы распределения характерна большая островершинность и более длинные хвосты на концах (рис. 6.3). По мере возрастная v распределение стремится к нормальному и уже при v = 30 t-распределение практически не отличается от него.

Рис. 6.3. Кривая нормального (1) и t-распределения (2).
t-распределение Стьюдента играет важную роль в гидрометеорологических исследованиях. Наибольшее распространение оно получило для оценки доверительных границ математического ожидания, оценки значимости среднего, оценки расхождения средних значений по двум и более рядам значений исследуемых процессов.
6.5.3. Определение доверительных границ математического
Ожидания
Пусть имеется выборка значений случайной величины Х объемом в п членов. Среднее значение выборки: 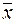 , несмещенная оценка дисперсии:
, несмещенная оценка дисперсии: 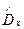 . На основании этих данных требуется найти границы, внутри которых с определенной степенью надежности находится среднее значение генеральной совокупности тx.
. На основании этих данных требуется найти границы, внутри которых с определенной степенью надежности находится среднее значение генеральной совокупности тx.
Выбрав двухсторонний 10 %-й уровень значимости (2α=10%), при данном числе степеней свободы v находим t0,05 такое, что 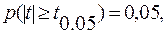 т. е. вероятность того, что |
т. е. вероятность того, что | 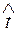 | будет больше или равно табличному t0,05 составляет 0,05. Тогда вероятность противоположного неравенства будет равна
| будет больше или равно табличному t0,05 составляет 0,05. Тогда вероятность противоположного неравенства будет равна 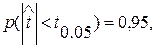 т. е. вероятность того, что t находится в пределах ± t0,05. составляет 90 %. Подставляя в это равенство значение t, находим
т. е. вероятность того, что t находится в пределах ± t0,05. составляет 90 %. Подставляя в это равенство значение t, находим
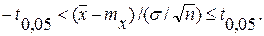 (6.24)
(6.24)
Отсюда
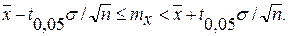 (6.25)
(6.25)
Таким образом, с вероятностью 0,90 можно утверждать, что среднее значение общей совокупности лежит между значениями 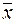 н и
н и 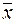 в, равными соответственно
в, равными соответственно
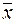 н =
н = 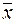 -t0,05σ/
-t0,05σ/ 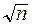 ,
, 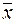 в =
в = 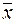 +t0,05σ/
+t0,05σ/ 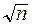 . (6.26)
. (6.26)
Эти значения называются доверительными границами среднего значения общей совокупности при двухстороннем 5%-м уровне значимости.
6.5.4. Оценка значимости среднего значения
Под значимостью среднего значения понимается существенность отличия среднего значения X по данной выборке (х1 x2,…., хп) от предполагаемого, исходя из тех или иных соображений, значения математического ожидания тх = т0. Отличие, того или иного знака, считается существенным (см. разд. 6.3), если вероятность его меньше заданного уровня значимости.
Схемаоценки значимости заключается в следующем.
1. Задается нулевая гипотезой, что математическое ожидание тх генеральной совокупности случайной величины X равно с, т. е. Н0 : тх =с.
2. По формуле ( ) рассчитывается нормированное отклонение среднего значения выборки 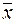 от с
от с
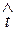 = (
= ( 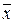 - с)/(σx/
- с)/(σx/ 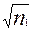 ) . (6.27)
) . (6.27)
3. Если нулевая гипотеза Hо верна, то распределение t должно подчиняться закону t-распределения Стьюдента. Находим по этому распределению вероятность полученного значения 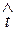 при данном числе степеней свободы
при данном числе степеней свободы 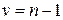 . Если эта вероятность окажется меньше заданного уровня значимости α, то гипотеза Hо опровергается, если больше α, то гипотеза не опровергается.
. Если эта вероятность окажется меньше заданного уровня значимости α, то гипотеза Hо опровергается, если больше α, то гипотеза не опровергается.
На практике при оценке значимости часто поступают несколько иначе. Вместо определения вероятности 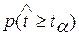 определяется критическое при проверке Hо значение статистики t: t = t2a и сравнивается с
определяется критическое при проверке Hо значение статистики t: t = t2a и сравнивается с 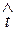 . Если
. Если 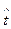 > t2α, то гипотеза опровергается.
> t2α, то гипотеза опровергается.
Дата добавления: 2020-10-25; просмотров: 575;











