Оценка расхождения между средними значениями

Часто в исследованиях встает вопрос о сравнении математических ожиданий двух случайных величин по их выборкам.

Пусть, например, имеются две независимые частичные совокупности объемов п₁ и п₂, взятые соответственно из генеральных совокупностей X и Y. Нулевая гипотеза состоит в предположении, что математические ожидания ряда X и Y равны, т. е. Н_о: т_х= т_у. В качестве критерия проверки Н_о естественно взять нормированную разность выборочных значений

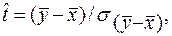
(6.27)

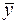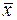где и — средние значения выборок У и X; 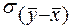— среднее квадратическое отклонение разности средних значений.

Если известны или предполагаются известными действительные значения средних квадратических отклонений рядов Y и X то среднее квадратическое отклонение разности выборочных средних 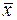и 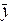,при условии независимости рядов X и Y, может быть определено, по формуле

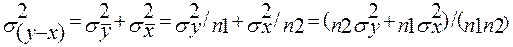(6.28)

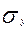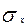В случае, если действительные значения и неизвестны, проверка H_о производится, как правило, на основе предположения, что 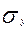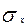₌ =σ . В этом случае из формулы (6.28) следует

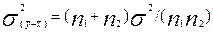, (6.29)

где σ определяется путем взвешивания по числу лет наблюдений

(6.30)

Из формул (6.27)—(6.30) получаем: для случая, когда 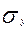и 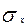известны:

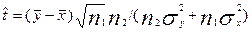, (6.31)

для случая, когда 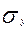и 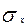не известны:

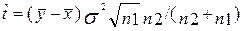(6.32)

где σ определяется по формуле (6.30).

Нормированная разность выборочных средних следует, как известно из работы [60], закону t-распределения Стьюдента при числе степеней свободы

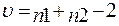(6.33)

Отсюда по таблице распределения t-статистики, так же как и в предыдущем случае, может быть определено критическое для данной гипотезы значение t_a при данном уровне значимости а.

Если значение 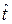окажется больше t_a при данном уровне значимо­сти а или p( 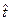>t_a) окажется меньше а, то гипотеза Н_о: т_у= т_x опровергается.

ОЦЕНКА ДИСПЕРСИИ

6.6.1. Постановка задачи

 

Оценка равенства действительных значений дисперсий по выборкам или отдельным частям одной выборки производится при помощи статистики F, называемой дисперсионным отношением:

 

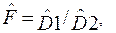(6.34)

 

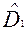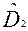где и _ выборочные значения дисперсий. При этом в числителе берется большее значение.

Функция обеспеченности статистики F, выражающая вероят­ность того, что значение 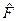будет больше или равно некоторому значению F

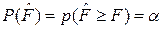, (6.35)

 

где а – уровень значимости, установлена Фишером.

Функция плотности вероятности этого распределения (F-распределение) описывается формулой

 

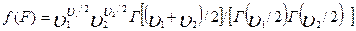
(6.36)

где и 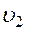— число степеней свободы первой и второй выборки:

 

υ ₁=n₁ – 1, υ₂ = n₂- 1 (6.37)

 

Как следует из формулы (6.36), F-распределение не зависит от дисперсии исходных рядов, а зависит только от числа степеней свободы. Это обстоятельство является очень важным, так как именно дисперсию и требуется установить в результате тех или иных исследований.

Для F-распределения составлены таблицы значений в зависимости от числа степеней свободы и уровней значимости. Имеются таблицы значений F, которые могут быть превзойдены с вероятно­стью а 0,05; 0,025; 0,01; 0,005, где число v₁ определяет столбец, a v₂ строку (см., например, работу [63], прилож. 8). В таблицах указаны значения для одностороннего критерия значимости, т. е. для оценки, например, D₁ > D₂. Если требуется оценить равенство дисперсий по двум выборкам, т. е. проверить D₁= D₂, то уровень значимости следует удвоить.

Для оценки доверительного интервала и значимости дисперсии используется отношение

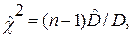
(6.38)

 

которое удовлетворяет 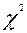- распределению с v = n—1 степенями свободы, если гипотеза Н_о: 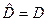верна [60].