Критерий Манна — Уитни

Манн и Уитни распространили указанный критерий Уилкоксона на сравнение двух независимых выборок. Этот критерий является наиболее распространенным и популярным ранговым критерием.

Значением критерия служит общее число инверсий U. Об инвер-

сии мы говорим, когда в упорядоченном ряде n₁+n₂ членов в порядке возрастания для произвольной пары (y_i, Х_k) выполня­ется соотношение x_k > y_i, т. е. когда у_i стоит перед х_k. Иначе го­воря, если какому-либо значению х в упорядоченном ряде пред­шествует у, то эта пара дает инверсию. Так, в последовательно­сти (6.47) x₁ и x₂ дают по одной инверсии с у₁; x₃ дает четыре инверсии с y₁, у₂, у₃, у₄ и х₄ дает шесть инверсий с y₁, у₂, у₃, у₄, y_5, y₆. Всего инверсий в перечисленных значениях упорядо­ченного ряда (6.48) будет

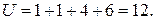
Теоретически доказано, что при объемах выборок n₁ > 10 и п₂ > 10 число инверсий U распределено приблизительно нор­мально с математическим ожиданием

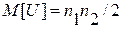(6.53)

и дисперсией

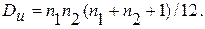(6.54)

Критическая область значений U для нулевой гипотезы об от­сутствии существенных различий в сопоставляемых выборках с учетом нормального закона распределения U может быть пред­ставлена в виде:

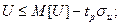(6.55)

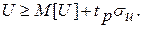(6.56)

Критерий знаков

Основан на учете различия между соответствующими значе­ниями ряда X и Y. Нулевая гипотеза состоит в предположении, что рассматриваемые ряды X и Y подчиняются одному и тому же закону распределения. Отсюда должно следовать, что разности ∆_i = x_i - y_i распределены симметрично около нуля, т. е. отклонение положительного и отрицательного знаков равновероятны. При этом, естественно, абсолютные величины разностей не имеют зна­чения, а разности, равные нулю, исключаются из рассмотрения.

Таким образом, сравнивая ряды X и Y, можно определить знак разности и подсчитать число случаев со знаком «плюс» и со зна­ком «минус». Затем наименьшее число случаев сравнивается с кри­тическим числом [63].

[A1]