Критерий Уилкоксона

В 1955 г. Уилкоксон предложил непараметрический метод про­верки гипотез, позволяющий осуществлять проверку зависимых вы­борок в тех случаях, когда данные измерений попарно взаимо­связаны.

Пусть даны две независимые выборки объема n₁ и п₂ (х₁, х₂, …, Х_n1 и у₁, у₂, …, y_n2). Требуется определить принадлеж­ность данных двух выборок к одной генеральной совокупности, т. е. проверить гипотезу H_о:F₁{x) =F₂(y). Так как критерий Уил­коксона принадлежит к категории ранговых критериев, то для его применения n₁+n₂ данных обеих выборок совместно упорядочиваются. Например, наблюдения, полученные в двух выборках, рас­полагаются в общую последовательность в порядке возрастания их значений

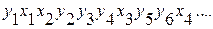(6.47)

Статистика ω критерия Уилкоксона задается выражением

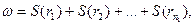
(6.48)

где r₁, r₂, …, r_n - ранги (порядковые номера), соответствующие значениям X; S - некоторая функция.

В выражении (6.48) ранги могут быть записаны следующим образом:

12345678910,

где для значений выборки X значения рангов будут

2, 3, 7, 10, ....

Выбор функции S(r) осуществляется так, чтобы чувствитель­ность критерия в данном конкретном случае была бы, по возмож­ности, наибольшей. Если математические ожидания X и Y не равны между собой, то целесообразно положить S(r)=r и вычис­лять ω по формуле

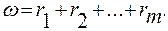(6.49)

Математическое ожидание и дисперсия статистики ω опреде­ляются по формулам:

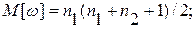(6.50)

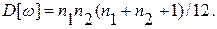(6.51)

Критические значения двухстороннего критерия Уилкоксона ω с уровнем значимости 2α определяются нижним и верхним пре­делом. Значения нижнего предела ω_н (α, п₁, п₂) при объемах вы­борок n₁ и n₂, не превышающих 25, приводятся в соответствующих таблицах (см., например, работу 3], прилож. 9).

Поскольку распределение статистики ω симметрично относи­тельно математического ожидания, то верхнее критическое значе­ние ω_в связано с ω_н следующим соотношением:

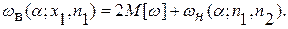(6.52)

Если n₁ или п₂ больше 25, то для вычисления критических зна­чений ω_н и ω_в используется нормальное распределение с парамет­рами, заданными формулами (6.51), (6.52).