ПРОВЕРКА ГИПОТЕЗ О ПАРАМЕТРАХ РАСПРЕДЕЛЕНИЯ

Постановка задачи

Действительные значения параметров распределения исследуемой случайной величины, как правило, неизвестны. В связи с этим при работе с эмпирическими данными возникают две задачи: 1) получить наиболее точное представление о параметрах распределения случайной величины по эмпирическим данным; 2) определить соотношение параметров распределения различных процессов или процессов в различные периоды времени по эмпирическим данным.

Для того, чтобы получить полное представление о точности и надежности статистической оценки 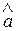параметра а необходимо для каждого малого α>0 указать такое δ, что

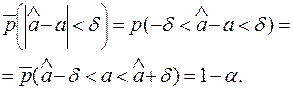(6.19)

Полученное уравнение есть вероятность того, что интервал ( 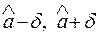) со случайными концами накроет неизвестный параметр с вероятностью 1-α. Это уравнение в отличие от основных погрешностей дает представление о вероятности того или иного значения параметра а при данном значении оценки 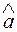. Чем меньше для данного а будет δ, тем точнее будет оценка .

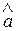Интервал (а-δ, α+ δ) со случайными концами с вероятностью, равной 1-α, покрывающий неизвестный параметр, называется доверительным интерваломпри данном уровне значимости α.

Для того, чтобы найти доверительный интервал какой-либо статистической характеристики, как следует из вышесказанного, необходимо прежде всего знать возможное распределение этой статистики. Именно поэтому главная задача статистического исчисления при малом числе наблюдений (ограниченный объем вы­борки) состоит в установлении точных распределений разных статистик. При таком толковании статистических оценок изменяются как сами вопросы, возникающие при исследовании точности расчетов, так и способы их решения.