Выбор закона распределения. Постановка задачи
В гидрометеорологических исследованиях используется целая группа законов распределения и созданных на их основе кривых обеспеченностей. Из них наибольшее распространение получили кривые обеспеченностей нормального закона распределения; распределения Пирсона III типа, Крицкого-Менкеля, Гумбела, Джонсона; логарифмически нормального закона и некоторых других. Описание этих законов распределения и кривых обеспеченностей дано в главе 4.
По имеющемуся ряду наблюдений необходимо выбрать один из перечисленных законов распределения. Однако для объективного суждения о лучшем или худшем соответствии того или иного закона распределения имеющимся данным наблюдений, особенно при ограниченном объеме выборок, необходимо иметь какой-то количественный показатель, который измерял бы степень случайного расхождения (или согласия) между наблюденным рядом и предполагаемым распределением случайной величины в целом. Такой показатель также, очевидно, должен являться случайной величиной.
Подобные показатели, называемые критериями соответствияили критериями согласия, представляют собой определенную меру расхождения между теоретическим (или гипотетическим) и эмпи  рическим распределением и основаны на непараметрической гипотезе вида (6.2). Если расхождение в рассматриваемом случае превосходит установленный предел, то гипотеза опровергается.
рическим распределением и основаны на непараметрической гипотезе вида (6.2). Если расхождение в рассматриваемом случае превосходит установленный предел, то гипотеза опровергается.
Имеется несколько видов критериев согласия, используемых в различных ситуациях.
6.4.2. Критерий согласия Колмогорова
В качестве показателя степени согласия эмпирической 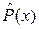 и теоретической Р(х) кривых обеспеченностей принята величина
и теоретической Р(х) кривых обеспеченностей принята величина
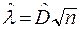 (6.4)
(6.4)
где 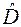 – наибольшая разность значений эмпирической
– наибольшая разность значений эмпирической 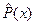 и теоретической обеспеченности:
и теоретической обеспеченности:
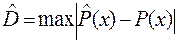 (6.5)
(6.5)
( 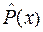 и Р(х) — в долях единицы). Очевидно, что
и Р(х) — в долях единицы). Очевидно, что 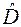 , являющееся функцией случайной величины
, являющееся функцией случайной величины 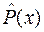 , также представляет собой значение случайной величины. Предельное распределение этой величины вне зависимости от гипотетического распределения, для условия, когда нулевая гипотеза верна, было установлено А. Н. Колмогоровым в следующем виде:
, также представляет собой значение случайной величины. Предельное распределение этой величины вне зависимости от гипотетического распределения, для условия, когда нулевая гипотеза верна, было установлено А. Н. Колмогоровым в следующем виде:
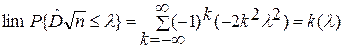 (6.6)
(6.6)
Отсюда при достаточно больших п вероятность получить значение 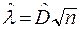 , большее, чем λ, равна 1 — k (λ), т. е.
, большее, чем λ, равна 1 — k (λ), т. е.
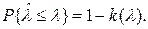 (6.7)
(6.7)
Значения вероятностей превышения 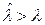 -Р =1—k(λ) для случая, если гипотеза (6.3) верна, табулированны [ ]. Задавая уровень значимости α = Р = 1- k(λ), можно по значению 1- k(λ) определять критические значения λα. Если рассчитанное значение
-Р =1—k(λ) для случая, если гипотеза (6.3) верна, табулированны [ ]. Задавая уровень значимости α = Р = 1- k(λ), можно по значению 1- k(λ) определять критические значения λα. Если рассчитанное значение 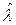 больше критического при данном уровне значимости, то гипотеза H0 опровергается, расхождение эмпирического и гипотетического распределения считается существенным.
больше критического при данном уровне значимости, то гипотеза H0 опровергается, расхождение эмпирического и гипотетического распределения считается существенным.
Если обеспеченность значения 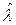 по кривой обеспеченностей λα = f (1-k(λ)) меньше, чем 1% и 0,1 %, то расхождение считается весьма существенным. В противном случае, т. е.
по кривой обеспеченностей λα = f (1-k(λ)) меньше, чем 1% и 0,1 %, то расхождение считается весьма существенным. В противном случае, т. е. 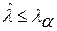 , гипотеза не опровергается, но это еще не значит, что она доказана.
, гипотеза не опровергается, но это еще не значит, что она доказана.
На основании формул (6.5) и (6.6) может быть получена формула для доверительных границ 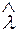 относительно гипотетического закона распределения в точке
относительно гипотетического закона распределения в точке 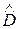
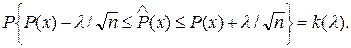 (6.8)
(6.8)
Если рассчитанное значение 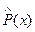 попадает в доверительный интервал, то гипотеза (6.2) не опровергается, если это значение попадает в критическую область, то гипотеза опровергается.
попадает в доверительный интервал, то гипотеза (6.2) не опровергается, если это значение попадает в критическую область, то гипотеза опровергается.
Практическое применение критерия согласия Колмогорова для оценки правильности гипотезы H0 состоит в следующем:
1) для отдельных значений ряда xi (i=1, 2, . . , п), расположенных в убывающем порядке, определяются (в долях единицы) эмпирические обеспеченности;
2) для этих же значений определяются обеспеченности по предполагаемой теоретической кривой обеспеченности
3) находится наибольшее значение разности 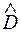 [ формула (6.4)] и
[ формула (6.4)] и 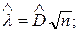
4) по кривой обеспеченностей или таблице значений 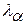 определяется обеспеченность
определяется обеспеченность 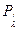 рассчитанного значения
рассчитанного значения 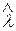 . Если
. Если 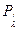 <α, то гипотеза H0 опровергается, в противном случае не опровергается.
<α, то гипотеза H0 опровергается, в противном случае не опровергается.
Критерий согласия Колмогорова, как следует из формулы(6.5), предназначен для случая, когда п достаточно велико. Однако исследования, выполненные в последнее время, показали, что распределение статистики 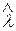 уже при п≥ 20 практически не зависит от п.
уже при п≥ 20 практически не зависит от п.
При небольших значениях п необходимо учитывать следующие обстоятельства
1) критерий согласия 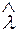 , определенный фактически по одной точке, в некоторых случаях может не отражать общую согласованность эмпирического и теоретического распределения;
, определенный фактически по одной точке, в некоторых случаях может не отражать общую согласованность эмпирического и теоретического распределения;
2) наибольшее значение 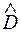 , как правило, отмечается в средней части кривой обеспеченностей. Однако именно в этой части почти все кривые обеспеченностей, используемые в практике, достаточно хорошо совпадают. Поэтому суждение о совпадении теоретических и эмпирических кривых обеспеченностей в краевых частях (именно это и нужно для практических расчетов) на основании критерия Колмогорова следует выносить очень осторожно.
, как правило, отмечается в средней части кривой обеспеченностей. Однако именно в этой части почти все кривые обеспеченностей, используемые в практике, достаточно хорошо совпадают. Поэтому суждение о совпадении теоретических и эмпирических кривых обеспеченностей в краевых частях (именно это и нужно для практических расчетов) на основании критерия Колмогорова следует выносить очень осторожно.
6.4.3. Критерий согласия Пирсона P[χ2]
Для оценки согласия эмпирических данных (x1, х2,…, хп) и предполагаемого закона распределения используется расхождение между эмпирической 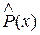 и теоретической Р(х) вероятностью отдельных значений или интервалов значений случайной величины.
и теоретической Р(х) вероятностью отдельных значений или интервалов значений случайной величины.
Если число значений дискретной случайной величины X ограничено (ξ1, ξ2,…,ξk) и каждое ξj (j=1, 2, …, k) встречается в выборке (имеющегося ряда наблюдений) не менее 5 раз, то расчеты критерия согласия производятся по вероятности, эмпирической и теоретической, каждого значения ξj.
Если X является непрерывной случайной величинойили возможное число значений X велико так, что каждое или некоторые значения ξ встречаются менее 5 раз, то необходимо использовать метод группировки данных и перейти к рассмотрению дискретной системы, в которой рассматриваются вероятности отдельных интервалов значений X.
Пусть имеется выборка x1, x2, ..., хп. Значения выборки оформлены в виде статистического ряда распределения (см. разд. 4.3), в котором указаны эмпирические вероятности 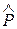 (относительная частота) отдельных значений или интервалов значений X. (Отдельные значения или интервалы значений X здесь и дальше обозначим через ζj (j=1, 2, …, k), через k- число отдельных значений или интервалов значений). Здесь же приводятся вероятности
(относительная частота) отдельных значений или интервалов значений X. (Отдельные значения или интервалы значений X здесь и дальше обозначим через ζj (j=1, 2, …, k), через k- число отдельных значений или интервалов значений). Здесь же приводятся вероятности 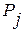 значений ζ j, определенные по предполагаемому теоретическому закону распределения.
значений ζ j, определенные по предполагаемому теоретическому закону распределения.
В качестве меры расхождения между теоретической и эмпирической вероятностью принимается сумма квадратов отклонений 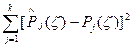 взятых с некоторыми весами Сj:
взятых с некоторыми весами Сj:
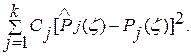 (6.9)
(6.9)
Веса Cj вводятся потому, что в общем случае относящиеся к различным разрядам отклонения нельзя считать равноправными по значимости. Действительно, одно и то же ∆Pj может быть малозначительным, если сама вероятность Pj(ζ) велика, и очень заметным, если она мала. Поэтому естественно, что Сj берутся обратно пропорциональными Pj(ζ). Пирсон показал, что закон распределения
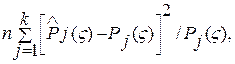
если нулевая гипотеза верна, обладает рядом интересных свойств: он практически не зависит от закона распределения X и от числа опытов п, а зависит только от числа к. При больших значениях п этот закон приближается к так называемому распределению χ2, т. е. можно принять, что
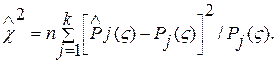 (6.10)
(6.10)
Распределением χ2 с v степенями свободы называется распределение суммы квадратов v независимых нормированных случайных величин, каждая из которых подчинена нормальному закону распределения с математическим ожиданием, равным нулю, и дисперсией, равной единице. Это распределение характеризуется плотностью вероятностей
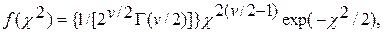 (6.11)
(6.11)
где v —число степеней свободы
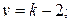 (6.12)
(6.12)
Г (v/2) —значение гамма-функции (см. гл. 4).
На основе формул (6.11) и (6,12) составлены таблицы значений χ2 для различных значений обеспеченности и числа степеней свободы (см., например, работу [ ], прилож. ). По этой таблице можно определить вероятность события 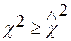 , где χ2 – значение, рассчитанное для данной нулевой гипотезы. Если вероятность окажется меньше заданного уровня значимости, то гипотеза опровергается. Аналогично можно сравнивать рассчитанное значение χ2 с табличным при данных v и α. Если
, где χ2 – значение, рассчитанное для данной нулевой гипотезы. Если вероятность окажется меньше заданного уровня значимости, то гипотеза опровергается. Аналогично можно сравнивать рассчитанное значение χ2 с табличным при данных v и α. Если 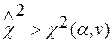 , то гипотеза опровергается.
, то гипотеза опровергается.
Для обоснованного применения критерия согласия χ2 необходимо иметь ввиду, что при выводе закона распределения χ2 предполагается, что биномиальное распределение частоты превышения 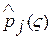 может быть сведено к нормальному. Однако соответствующий предельный переход осуществляется достаточно быстро, если ни одна из вероятностей
может быть сведено к нормальному. Однако соответствующий предельный переход осуществляется достаточно быстро, если ни одна из вероятностей 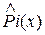 или Pi(x) не очень мала. Поэтому при практическом применении критерия согласия Р (χ2) необходимо частоты крайних разрядов, представляющих обычно малые числа, объединять между собой.
или Pi(x) не очень мала. Поэтому при практическом применении критерия согласия Р (χ2) необходимо частоты крайних разрядов, представляющих обычно малые числа, объединять между собой.
Считается, что использование распределения χ2 в качестве критерия согласия возможно только в тех случаях, когда длина выборки п ≥ 50, а частота отдельных значений или интервалов значений X (в том числе полученная за счет объединения крайних интервалов) не меньше 5.
Недостатком метода является то, что группировка данных по интервалам в случае непрерывной случайной величины или большого числа возможных ее значений приводит к некоторой потере информации. Кроме того, элементы неопределенности и возможной неоднозначности решений вносятся при назначении числа интервалов и длины самих интервалов.
К достоинствам критерия χ2 следует отнести универсальность — независимость от закона распределения; возможность использования для данных нечислового характера; состоятельность.
В некоторых случаях, для оценки согласия законов распределения по критеоию Пирсона можно воспользоваться предложением В. А. Романовского. Он предложил простое правило, в значительной степени облегчающее применение критерия согласия Пирсона. Это правило основывается на том, что
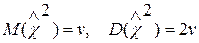 (6.13)
(6.13)
и вероятность значений χ2, отклоняющихся от М(χ2), меньше, чем на 3 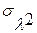 , т. е. на 3
, т. е. на 3 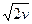 в ту или другую сторону, близка к единице. Отсюда, если
в ту или другую сторону, близка к единице. Отсюда, если
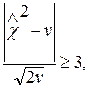
| (6.14) |
то расхождение можно считать существенным, гипотеза опровергается, в противном случае — гипотеза не опровергается (при уровне значимости 0,3 %).
6.4.4. Критерий согласия пω2
Критерий согласия пω2 в отличие от критерия χ2 основывается на оценке расхождения обеспеченностей непосредственно наблюденных (несгруппированных) значений рассматриваемой величины X.
Расчет критерия пω2 производится по формуле
 (6.15)
(6.15)
где
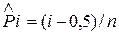 , (6.16)
, (6.16)
и Pi — соответственно значения обеспеченности по эмпирической и предполагаемой теоретической кривым обеспеченностей для каждого данного хi (i =1, 2, …, п). Математическое ожидание и дисперсия пω2 равны:
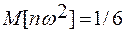 (6.17)
(6.17)
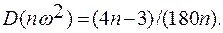 (6.18)
(6.18)
В случае, если гипотеза верна, при увеличении числа опытов ω2 сходится к нулю, а nω2 к 1/6 и при п ≥40 распределение произведения nω2 2 близко к некоторому предельному распределению, для которого определены верхние доверительные границы критерия nω2 (табл. 6.1).
Таблица 6.1 – Значения верхних доверительных границ критерия nω2 в зависимости от уровня значимости α, %.
| α | 0,1 | ||||||
| nω2 | 0,2412 | 0,3473 | 0,4614 | 0,5489 | 0,6198 | 0,7435 | 1,168 |
Для оценки гипотезы о законе распределения при использовании критерия nω2 необходимо:
1) ранжировать исходный ряд в убывающем порядке;
2) рассчитать эмпирические обеспеченности X по формуле (6.18);
3) определить обеспеченности значений xi по предполагаемому закону распределения;
4) рассчитать критерий nω2;
5) сопоставить рассчитанное значение nω2 с критическим nω2α при данном уровне значимости а. Если 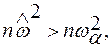 то гипотеза (6.2) о согласии кривых обеспеченности опровергается.
то гипотеза (6.2) о согласии кривых обеспеченности опровергается.
Критерий nω2 обладает рядом преимуществ по сравнению с критерием χ2. Во-первых, при его применении полнее используется информация, заключающаяся в данных выборки, так как его расчет основывается на анализе непосредственно наблюденных величин. Во-вторых, его распределение значительно быстрее сходится к предельному закону, особенно при больших значениях nω2.
Дата добавления: 2020-10-25; просмотров: 611;











