При помощи критерия значимости нулевая гипотеза может быть опровергнута. Но даже если гипотеза не опровергнута, это еще не значит, что она верна (см. рассмотренный выше пример).

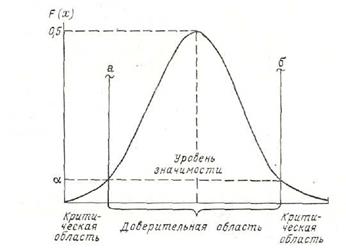
Рис. 6.1. Двухсторонний уровень значимости и доверительная область симметричного распределения: а — область положительных отклонений от среднего, б — область отрицательных отклонений.

На это необходимо обратить особое внимание. Только в случае достаточно высокой вероятности полученного результата при данной нулевой гипотезе можно утверждать, что рассматриваемая гипотеза, по-видимому, верна.

Выбор уровня значимости или вероятности события, которой решено пренебречь в данной области исследования, производится в некоторой степени произвольно. Он устанавливается на основании опыта, как уровень, дающий определенную практическую уверенность, что ошибочные заключения будут сделаны только в очень редких случаях. Например, в расчетах и прогнозах широко используются 10, 5, реже используется 1 %-й уровень значимости (α = 10, 5, 1 %). В других областях научных исследований уровень значимости может быть другим.

Следует отметить, что при увеличении уровня значимости (рис. 6.1) увеличивается критическая область, а следовательно, возрастает и вероятность попадания исследуемой статистики в критическую область. Вместе с тем, очевидно, возрастает и вероятность ошибочного отбрасывания гипотезы. Действительно, при уровне значимости α, равном, допустим, 20 %, будут опровер­гаться все гипотезы, вероятность статистик которых составляет 20 % и менее. Однако значение этих статистик и в этом случае, если гипотеза верна, возможно в среднем в одном из пяти случаев. Поэтому к отбрасыванию гипотез при больших уровнях значимости надо подходить очень осторожно.

С уменьшением уровня значимости возрастает число испытаний, необходимых для эффективного применения критерия значимости, так как при малом объеме выборок п возможна такая ситуация, когда гипотеза вообще не может быть опровергнута.

В качестве основного критерия при выборе того или иного уровня значимости выступает только возможность его использования на практике. С одной стороны, этот уровень должен быть достаточно велик для отбрасывания ложных гипотез, а с другой — он должен быть достаточно мал, чтобы приводить к отбрасыванию лишь немногих верных гипотез. Поэтому в каждой области исследований обычно вводится несколько уровней значимости и в каждом конкретном случае надо выбирать тот из уровней, который наиболее отвечает задаче данного исследования.

При этом, при всех прочих условиях, необходимо учитывать следующие важные обстоятельства.

1. Уровень значимости уменьшается с повышением важности расчета. Так, если проверяются, например, гипотезы о надежности или возможности отказа какой-то важной конструкции, то уровень значимости может быть принят равным даже 0,1 %.

2. Уровень значимости должен быть в какой-то степени согласован с точностью исследуемых исходных данных и возможностью увеличения объема выборки. Так как в гидрологии точность измерений, как правило, не превышает 5 %, то использование уровня значимости меньше 5 % не всегда достаточно обосновано.

При проверке гипотез необходимо различать двухсторонний (2α) и односторонний уровень значимости. Так, если при сравнении двух случайных величин требуется оценить их расхождение, т.е. одинаковый интерес представляют как положительная, так и отрицательная разность между изучаемыми величинами, то, допустим, при 5 %-м уровне значимости, берется по 2,5 % на каждом конце (рис. 6.2). Наиболее часто эта ситуация встречается при проверке средних значений, когда одинаково важны большие отклонения как в положительную, так и в отрицательную сторону.

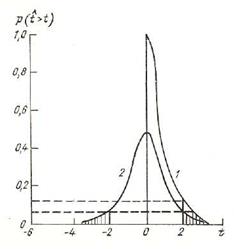
Рис. 6.2. Односторонний (1) и двух­сторонний (2) критерий значимости.

Односторонний критерий значимости используется в тех случаях, когда надо убедиться, что одно значение строго больше (меньше) другого.

При проверке гипотез возможны погрешности двух родов. Погрешность первого рода состоит в том, что нулевая гипотеза отвергается в то время, когда она в действительности верна. Чем меньше уровень значимости, тем меньше вероятность отвергнуть верную гипотезу.

Погрешность второго рода состоит в том, что нулевая гипотеза принимается, а на самом деле она неверна. Критерий значимости указывает на величину риска сделать погрешность первого (второго) рода.

6.4. Проверка гипотез о законе распределения