Критерий значимости

Понятие гипотез

Гипотеза — определенное представление или предположение относительно объективных свойств изучаемого явления.

Нулевая гипотеза – гипотеза, имеющая в данном случае особенно важное значение, называется нулевой или основной.

Гипотеза обычно обозначается через Н, нулевая гипотеза через Н₀.

Если закон распределения задан отдельными параметрами и гипотеза строится именно по этим параметрам (закон распределения рассматриваемых случайных величин предполагается известным), то говорят о параметрических гипотезах. Например, какое-либо допущение о неизвестном параметре распределения а закона Пирсона III типа является параметрической гипотезой. Символически ее можно записать так

Н₀ : a =c, (6.1)

где с — предполагаемое действительное значение параметра а.

Статистические гипотезы, в основе которых лежит предположение о конкретном виде распределения, называются непараметрическими. Символически эти гипотезы за­писываются в следующем виде:

H₀: F(x) = F_c(x). (6.2)

Непараметрические гипотезы являются более общими, чем параметрические. Более общими и менее эффективными являются и методы их проверки.

Рассмотрим принципиальную схему статистической проверки гипотез на примере параметрической гипотезы.

Проверка как параметрических, так и непараметрических гипотез чаще всего основывается на использовании хорошо изученных законов распределения некоторых статистик. Например, нормированная разность средних значений рядов Y и X, соответственно 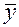и

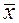
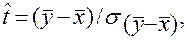(6.3)

где 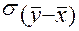– среднее квадратическое отклонение разности 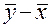, подчиняется закону распределения Стьюдента–Госсета (см. раздел 6.5). С помощью этого закона в данном случае можно определить вероятность равенства действительных значений математического ожидания сопоставляемых выборок Y и X

Таким образом, применение нулевой гипотезы H₀:a=с позволяет воспользоваться известным распределением выборочных оценок статистики с и по этому распределению оценить вероятность 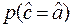при условии, что а = с.

Сразу отметим, что в данном случае закон распределения выборочных значений известной статистики с является тойдополнительной информацией, которую получают за счет использования нулевой гипотезы.

Пусть, например, имеются предположения, что математические ожидания рядов Х₁ и Х₂ (соответственно т₁ и т₂) совпадают с математическим ожиданием генеральной совокупности X m_x = 200 м³/с, т. е.

H₀₁ : m₁ =m_x = 200 м³/с;

H₀₂ : m₂ =m_x = 200 м³/с.

Продолжительность периода наблюдений по рядам Х₁ и Х₂: n₁ = n₂ = 100 лет. Ряды Х₁, Х₂ и генеральная совокупность подчи­няются нормальному закону распределения. Известно также, что σ₁= σ₂= σ_x= 100 м³/с, 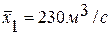, 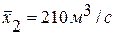. Оценим насколько верны эти гипотезы.

Если эти гипотезы верны, то учитывая одинаковый закон распределения сопоставляемых рядов Х₁, Х₂, X и равенство средних квадратических отклонений, принимаем, что функции распределения (обеспеченности) средних столетних зна­чений по названным рядам одинаковы, т. е. 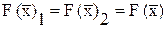. Тогдапо функции распределения 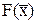можно оценить вероятность зна­чений 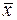, больших или равных 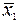и 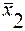. Координаты кривой обеспеченности нормального закона распределения заданы в нормированном виде (6.3)

где 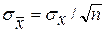. Находим теперь t no 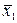= 230 м³/с и 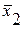= 210 м³/с. Получаем 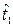= 3,0, 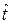₂=1,0 и находим вероятность их превышения по заданным координатам:

,

.

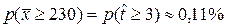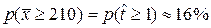Таким образом, при условии, что т_х = 200 м³/с вероятность получить выборочное значение 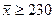составляет всего 0,11 %, т.е. очень мала. Получить событие с такой вероятностью в одном ис­пытании практически невозможно. А так как оно получено, то, по-видимому, неверно рассчитана его вероятность. В свою очередь вероятность события 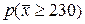вычислялась на основе гипотезы Н₀₁. Все это позволяет нам утверждать, что сама гипотеза неверна.

Вероятность получить выборочное значение 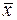₂ =210 м³/с составляет 16 %, т. е. достаточно велика, опровергать гипотезу у нас нет оснований. С другой стороны, это еще не означает, что гипотеза верна, так как вероятность события 16 % недостаточна для такого утверждения.

В данном случае бы рассмотрен простейший случай проверки статистической гипотезы, когда сам процесс проверки и интерпретации ее результатов не вызывали особых трудностей. Во многих случаях проверка гипотез имеет гораздо более сложный характер, тогда необходимо создание специальных правил проверки гипотез.

Правило, согласно которому проверяемая гипотеза H_о принимается или опровергается, называется статистическим критерием или просто критерием проверки гипотез.