О НЕКОРРЕКТНОСТИ ОПЕРАЦИИ ЧИСЛЕННОГО

ДИФФЕРЕНЦИРОВАНИЯ

Итак, при уменьшении шага h погрешность аппроксимации (то есть погрешность метода) уменьшается. Но погрешность решения включает в себя не только погрешность метода, но и погрешность исходных данных, и вычислительную погрешность (см. п.1.1).

Численное дифференцирование относится к таким задачам, в которых погрешность, возникающая при вычислении разностных отношений, может неограниченно возрастать при стремлении шага сетки h к нулю. Поэтому операцию вычисления разностных отношений называют некорректной.

Рассмотрим причину некорректности на примере вычисления разностного отношения

y¢_i » (y_i–y_i–1)/h ,

представляющего собой формулу левых разностей. Погрешность аппроксимации первой производной составляет

R = M₂h/2,

то есть прямо пропорциональна шагу в первой степени.

С другой стороны, значения функций y_i и y_i–1 вычисляются, вообще говоря, с некоторой погрешностью, то есть

.

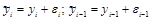Поэтому реально мы найдем

.

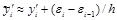Пусть |e_i| £ e; |e_i–1| £ e, где e – верхняя грань погрешностей. Тогда получается, что абсолютную погрешность производной y¢_i можно оценить по формуле

a = 2e /h.

Итак, если перейти к обозначениям п.1.1, то R º e₂ , а a º e₃. Следовательно, при h® 0 погрешность метода e₂®0 , а вычислительная погрешность e₃ ® ¥ (см. рис.3.1).

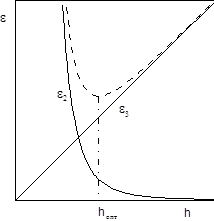
Рис.3.1 – Ошибка численного дифференцирования

Суммарная же погрешность e_S = M₂h/2 + 2e /h (пунктирная линия) может убывать при уменьшении шага лишь до некоторого предельного значения h_опт.

Таким образом, если нет возможности менять величину e, то вычисления производной надо проводить не с произвольным шагом h, а с шагом, удовлетворяющим условию

h » h_опт , где h_опт =2 .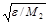

Отметим, что при вычислении производных более высокого порядка, когда в знаменатель входит h^k (k>1), влияние погрешности в определении y_i сказывается еще больше.