С помощью интерполяционного полинома Ньютона

Построим для заданной функции интерполяционный полином Ньютона:

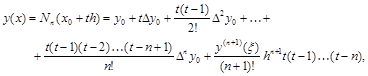
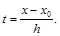
Тогда аппроксимация первой производной имеет вид:

,

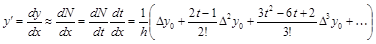аппроксимация второй производной:

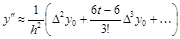и так далее.

Это так называемые конечно-разностные формулы численного дифференцирования. Безразностные формулы можно получить, выразив разности через значения функции (2.7).

Ясно, что для аппроксимации производных больших порядков необходимо привлекать все больше и больше узловых точек.

Оценка погрешности получается аналогично – как соответствующая производная от погрешности интерполяционного полинома Ньютона.

Например,

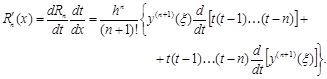
Так как формулы численного дифференцирования обычно используют в узловых точках, то второе слагаемое в этой формуле обращается в нуль, и она принимает вид:

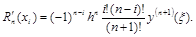
Пример 2. Получить аппроксимацию первой производной в точке х₀ по трем узловым точкам.

При х=x₀ t=0. Тогда для n=2

.

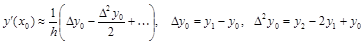Или, в безразностном виде,

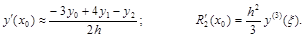
Примечание 2. Об узлах.

Все вышеприведенные формулы были записаны для случая равномерного расположения узлов. Их применение для произвольного неравномерного расположения узловых точек часто приводит понижению точности и даже к грубым ошибкам.

Конец примечания 2.