С помощью интерполяционного полинома Лагранжа

Построим для заданной функции интерполяционный полином Лагранжа

.

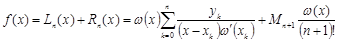Тогда

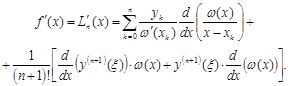
Получили формулу численного дифференцирования для первой производной по (n+1)-ой точке. Погрешность этой формулы состоит из двух слагаемых. Очевидно, что при оценке погрешности в узлах интерполяции х=х_k, первое слагаемое обращается в нуль, и тогда главный член погрешности имеет вид

.

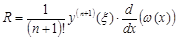Аналогично получаются формулы численного дифференцирования для производных более высоких степеней.

Пример 1.Получить формулу численного дифференцирования для производной 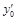по трем равноотстоящим узлам (n=2).

Интерполяционный полином Лагранжа при n=2 для равноотстоящих узлов будет иметь вид (см. пример из п.2.7):

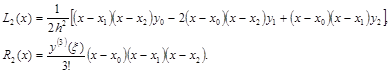
Тогда

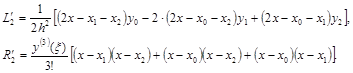
Эти формулы дают выражение для аппроксимации первой производной со вторым порядком. Они справедливы для любого хÎ[x₀; x₂], но чаще используются для узловых точек:

– при х=х₀ получаем требуемую формулу:

;

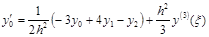– полагая х=х₁ и х=х₂ , можно получить другие формулы численного дифференцирования для первой производной по трем точкам:

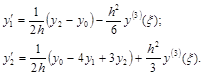
Записывая интерполяционный полином Лагранжа для четырех узлов (n=3), получаем формулы для аппроксимации первой производной с третьим порядком аппроксимации и так далее.

Таким образом, используя значения функции в n+1 узле, получаем производные с n-ым порядком аппроксимации.

Примечание 1. О центральных разностях.

Если для аппроксимации производной используются центральные разности, то, как это видно из примера, того же самого порядка аппроксимации можно добиться, используя число точек на единицу меньшее, чем при использовании нецентральных разностей.

Конец примечания 1.