МЕТОД РУНГЕ ОЦЕНКИ ПОГРЕШНОСТИ И
ПОЛУЧЕНИЯ ФОРМУЛ ЧИСЛЕННОГО
ДИФФЕРЕНЦИРОВАНИЯ
Как видно из вышеизложенного, порядок точности аппроксимации производных прямо пропорционален числу табличных узлов, используемых при аппроксимации. Следовательно, увеличить точность можно только за счет увеличения числа узлов.
Метод Рунге позволяет уточнять найденное значение для производной, а также, отталкиваясь от некоторой исходной формулы численного дифференцирования, получать формулу, порядок которой на единицу выше.
Введем некоторые условные обозначения.
Пусть F(x) – производная, подлежащая аппроксимации, а f(x,h)– некоторая конечно-разностная аппроксимация p-ого порядка этой производной на равномерной сетке с шагом h, то есть F(x)=f(x,h)+R, где R=hpj(x)+o(hp+1).
Здесь 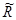 =hpj(x) называется главным членом погрешности.
=hpj(x) называется главным членом погрешности.
Запишем это же соотношение в той же точке х при другом шаге h1=kh , где k – некоторая целая константа:
F(x)=f(x,kh)+(kh)pj(x)+o((kh)p+1).
Приравнивая, получаем выражение для оценки главного члена погрешности (первая формула Рунге):
 (3.4)
(3.4)
Подставляя ее в предыдущую формулу, получаем вторую формулу Рунге :
F(x)=f(x,h)+  (3.5)
(3.5)
Эта формула позволяет по результатам двух расчетов значений производной f(x,h)и f(x,kh) с порядком аппроксимации p найти ее уточненное значение с порядком p+1.
Пример 4. Пусть функция y=lg(x) задана таблицей (см. с. 72). Найдем y¢(3). Для контроля: значение, полученное взятием производной, y¢(3) » 0,145. Для аппроксимации первой производной используем формулу центральных разностей (p=2; h=1):
| x | y=lg(x) |
| 0,301 | |
| 0,478 | |
| 0,602 | |
| 0,699 |
 Увеличим шаг вдвое (k=2):
Увеличим шаг вдвое (k=2):
 Оба полученных значения заметно отличаются от контрольного.
Оба полученных значения заметно отличаются от контрольного.
Используем для уточнения вторую формулу Рунге:

 .
.
Это значение всего на 2% отличается от контрольного.
Пример 5. Получим формулу второго порядка аппроксимации из формулы первого порядка.
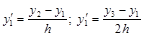 – две формулы первого порядка, отличающиеся шагом (к=2). Уточняем по методу Рунге:
– две формулы первого порядка, отличающиеся шагом (к=2). Уточняем по методу Рунге:
 .
.
Дата добавления: 2020-10-25; просмотров: 878;











