МЕТОД НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ
ПОЛУЧЕНИЯ ФОРМУЛ ЧИСЛЕННОГО
ДИФФЕРЕНЦИРОВАНИЯ
Другой способ построения формул численного дифференцирования – метод неопределенных коэффициентов.
Суть его заключается в следующем.
Искомое выражение для производной i-ого порядка в некоторой узловой точке x=xk представляется в виде линейной комбинации заданных значений функции в узлах x0, x1, ..., xn :
 ,
,
где Сj – некоторые пока не определенные коэффициенты.
Потребуем, чтобы эта формула была точна для полиномов возможно больших степеней  n, то есть чтобы при подстановке в нее полиномов, например, вида
n, то есть чтобы при подстановке в нее полиномов, например, вида
у=1; y=x–xk ; y=(x–xk)2; y=(x–xk)3 ;... ; y=(x–xk)n ,
она обращалась в точное равенство:
 .
.
Этим свойством обладают все формулы численного дифференцирования, в чем легко убедиться, подставляя поочередно полиномы вида у=1; y=x–x1; y=(x–x1)2
в формулу численного дифференцирования примера 2.
Полином 3-ей степени y=(x–x1)3уже не дает точного равенства.
Таким образом, для нахождения коэффициентов Сj (j=0...n) некоторой формулы численного дифференцирования получаем систему из (n+1) линейных алгебраических уравнений.
Следующая задача – определение погрешности формулы численного дифференцирования R.
Это можно сделать, например, разложением в ряд Тейлора значений функции y(x) в точке x=xi , но предлагаемый способ позволяет найти погрешность, продолжая процесс подстановки полиномов.
Основная идея заключается в том, что для степеней полиномов больших, чем n, формула численного дифференцирования возможно[1] будет уже неточной, то есть
 .
.
Поэтому, найдя коэффициенты Сj, продолжаем подставлять полиномы более высоких степеней y=(x–xk)m, где m>n, и определять R. Первое, отличное от нуля, значение R и будет погрешностью формулы численного дифференцирования, правда, пока для конкретного полинома степени m, то есть  .
.
Пересчет на погрешность для произвольной функции y проводится по формуле
 .
.
Пример 3.Найти выражение для производной 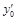 в случае трех равноотстоящих узлов:
в случае трех равноотстоящих узлов:
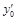 » C0y0+ C1y1+ C2y2 .
» C0y0+ C1y1+ C2y2 .
Используем следующие многочлены: у=1; y=x–x0; y=(x–x0)2:
при у=1 0= C0×1+ C1×1+ C2×1;
при y=x–x01= C0(x0–x0) + C1(x1–x0)+ C2(x2–x0);
при y=(x–x0)20= C0(x0–x0)2 + C1(x1–x0)2+ C2(x2–x0)2.
Заменяя разности в скобках их выражениями через шаг таблицы, получаем систему уравнений:
| Решение имеет вид: С0= –3/(2h); C1=4/(2h); C2= –1/(2h). |

Следовательно,

Найдем погрешность этой формулы.
При y=(x–x0)3  .
.
Тогда  , а Ry=2h2y(2)(x)/6 = h2 y(2)(x)/3.
, а Ry=2h2y(2)(x)/6 = h2 y(2)(x)/3.
Дата добавления: 2020-10-25; просмотров: 801;











