Получение формул численного дифференцирования

ПОЛУЧЕНИЕ ФОРМУЛ ЧИСЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ ПУТЕМ АППРОКСИМАЦИИ

Численным дифференцированием пользуются для отыскания производной функции, заданной таблично, а также для приближенного вычисления производной аналитически заданной функции, непосредственное дифференцирование которой затруднительно.

Основная идея получения формул численного дифференцирования состоит в том, что данная функция (табличная или аналитическая) заменяется некоторой аппроксимирующей функцией

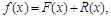
которая затем дифференцируется нужное число раз:

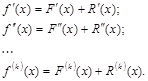
Получение формул численного дифференцирования с помощью

Рядов Тейлора

Пусть функция y=f(x) задана таблично, то есть

y_k = f(x_k), …, k=0, 1, ..., n.

Запишем ряд Тейлора

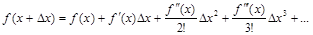
при х=х₁, Dх= – h, ограничившись первыми двумя членами:

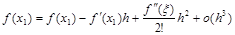
или, в других обозначениях,

.

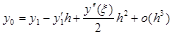Отсюда получаем формулу левых разностей

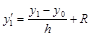, (3.1)

где 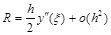= h^pj(х)+o(h^p+1) – погрешность аппроксимации: первый член называется главным членом погрешности, p – порядок аппроксимации производной. В данном случае h=1, таким образом, формула имеет первый порядок аппроксимации.

Если положить х=х₁, а Dх=h, то получается другая формула численного дифференцирования – формула правых разностей, тоже имеющая первый порядок аппроксимации:

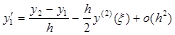. (3.2)

Если ограничиться четырьмя членами разложения, то для Dх=h и Dх= – h соответственно, можно записать

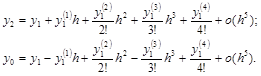
При вычитании получается формула центральных разностей второго порядка аппроксимации:

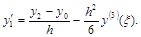(3.3)

При сложении получается формула численного дифференцирования для второй производной со вторым порядком аппроксимации:

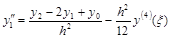. (3.4)

Аналогично можно получить аппроксимации производных более высокого порядка и оценку их погрешности. Но этот способ неудобен для практического использования, так как плохо алгоритмизируется и трудоемок.

Получение формул численного дифференцирования