Определения и обозначения

Случайные величины и их характеристики

Одним из основных понятий теории вероятностей является понятие случайной величины. Со случайными величинами приходится иметь дело в самых разнообразных областях науки и техники. Во многом на этом понятии основываются и методы обработки и анализа геоэкологической информации

Определения и обозначения

Существует множество определений этого понятия. В технических приложениях теории вероятностей обычно используются следующие определения

Cлучайная величина - величина, которая в результате испытания может принимать различные значения в зависимости от случайного исхода испытания.

или

Cлучайная величина - величина, которая в результате опыта может принять одно из возможных значений, неизвестно заранее какое именно

Следует обратить внимание на то, что это чисто математическое понятие. В этих определениях ничего не говорится о происхождении отдельных значений случайной величины. Случайны они в житейском смысле или достаточно точно определены внешними причинно-следственными связями в данном случае безразлично. Может быть и то и другое. Важно лишь то, что, зная п предшествующих значений случайной величины, мы не можем сказать какое из возможных значений примет ее п+i значение, где i может быть равно 1,2 и т. д.

Случайные величины могут быть одномерными и многомерными.

Одномерная случайная величина – величина, которая в результате испытания может приобретать только одно возможное значение

Многомерная случайная величина –величина, которая в результате испытания может принимать два и более возможных значения

Одномерная случайная величина, а следовательно, и процесс, который пред­ставляют в качестве последовательности значений одномерной случайной величины, обычно обозначается прописной латинской буквой X, Y и т. д. Последовательность значений случайной величины, принимаемая ею в результате опыта, обозначают строчными буквами с опущенным индексом х₁, х₂, . . ., х_п, где 1, 2, ..., п — номер испытания.

Например, процесс изменения годовых сумм осадков X в каком-то конкретном пункте за имеющийся период наблюдений в п лет может быть представлен последовательностью значений х₁, х₂, . . ., х_п, или в другой записи x_i (i = 1, 2, .. ., п).

Примером многомерной случайной величины может служить распределение дождевых осадков в каком-то районе. В этом районе имеется т пунктов наблюдений с периодом наблюдений п лет.

Тогда ряд наблюдений в первом пункте: х₁₁, х₁₂, . . .. х_1п или х_1i (i = 1, 2, . . ., п); соответственно в j-м пункте: x_j1, x_j2, …, x_jn или х_п (i = 1, 2, . .,, n) и в m-м пункте x_m1, x_m2, . . ., x_mn или x_mi (i = 1, 2, ..., n).

Например, в общем виде осадки в каком-то районе могут быть представлены в виде таблицы:

x ₁₁ x₁₂ … x_1i … x_1n

x ₂₁ x₂₂ … x_2i … x_2n

……………………… (3.1)

x _j1 x_j2 … x_ji … x _jn

_{....................................................}

x _m1 x_m2 … x_mi x_2n ,

которая называется матрицей наблюдений.

В краткой записи данные этой таблицы обозначаются

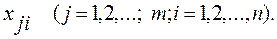(3.2)