Нормированная (стандартизованная) случайная величина

Во многих практических задачах, например, при сопоставле­нии асимметричности рядов стока и их законов распределения, формализованной записи того или иного ряда распределения тре­буется освободиться от влияния среднего значения т_х и среднего квадратического отклонения σ_х. Это достигается нормированием значений случайной величины.

Нормированной случайной величиной называется переменная вида

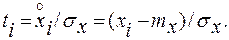
(3. 52)

Если X существенно положительно (X ≥ 0) то, разделив чис­литель и знаменатель на т_х, получим

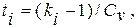
(3.53)

где k_i=x_i/m_x — модульный коэффициент.

Последовательность нормированных случайных величин обла­дает рядом замечательных свойств.

1. Математическое ожидание нормированной случайной величины равно 0, т. е. m [t] = 0. Действительно

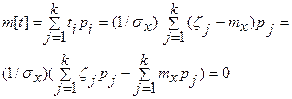(3.54)

2. Дисперсия нормированной случайной величины равна еди­нице, т. е. D_t =1. Действительно

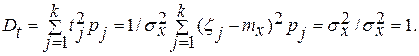
(3.55)

3. Если X — нормально распределенная случайная величина с параметрами т_х и σ², то нормированная случайная величина Т, представленное значениями t_i (i= 1,2, ..., N), также распределена нормально и имеет параметры 0 и 1.