Дискретные и непрерывные случайные величины

Различают два типа случайных величин: непрерывные и дискретные.

Непрерывная случайная величина может принимать любые численные значения в некотором диапазоне, который, в частности, может быть и бесконечным. Примером непрерывной случайной величины служат многие характеристики стока; средний годовой, максимальный, минимальный и т. д. Значения этих характеристик могут быть по сути дела любыми в заданном интервале.

Дискретная случайная величина может принимать только конечное или счетное множество значений. Значения, которые принимает дискретная случайная величина в результате опыта будем обозначать через ζ.

Примером дискретной случайной величины служит современная шкала облачности. Как известно, облачность измеряется в баллах от 0 до 10. В соответствии с этим и ряд наблюдений значений облачности может состоять только из следующих чисел: 0, 1, 2, ..., 10, каждое из которых может повторяться множество раз

На практике непрерывные случайные величины, учитывая точность измерений и необходимые округления, часто заменяются дискретными. Например, значения стока регистрируются с точностью до трех значащих цифр. Следовательно, период дискретности значения стока, например, при изменении его от 10,0 до 99,9 равен 0,1.

Рассмотрим одномерную дискретную случайную величину X, которая имеет к возможных значений ζ₁, ζ₂, …, ζ_к. События, в результате которых X примет каждый раз одно и только одно из возможных значений ζ _i (i = 1, 2, . . ., к), являются несовместными (никакие два из них не могут появиться вместе) и образуют полную группу событий (в результате опыта непременно должно появиться хотя бы одно из них). Каждое из этих событий возможно, но не достоверно, т. е. X может принять каждое из них с какой-то вероятностью р. Обозначим вероятность события X = ζ_i , т. е. р(Х= ζ_i ), через р_i . Так как множество всех несовместных событий образуют полную группу, то

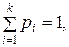(3.3)

т. е. сумма вероятностей всех возможных значений случайной величины равна 1.

Так, например, в каждый данный момент времени обязательно наблюдается одно из значений облачности от 0 до 10. Представляет практический интерес вероятность каждого из этих значений облачности, то есть, каким образом вероятность, равная 1, распределена между отдельными возможными значениями облачности. Конечно, было бы лучше если бы было указано точное значение облачности, допустим на завтра, однако (см. главу 3), такие прогнозы чаще всего невозможны. Поэтому на практике приходится обходится именно такой вероятностной оценкой случайной величины.

Считается, что случайная величина полностью описана с вероятностной точки зрения, если задана вероятность каждого из ее возможных значений. Этим устанавливается так называемый закон распределения случайной величины.