Числовые характеристики случайных величин
Полное представление о случайной величине дает ряд распределений или функция распределения. Однако ряд и функция распределения слишком громоздки и неудобны для практического использования, особенно при сравнительном анализе различных рядов наблюдений. Между тем, во многих случаях бывает вполне достаточно указать только отдельные параметры, характеризующие какие-либо существенные в данном случае черты распределения исследуемой случайной величины. Например, среднее значение, относительно которого располагаются все возможные значения случайной величины; характеристики рассеивания этих значений относительно среднего и т. д.
Следует также отметить, что при описании конкретных рядов наблюдений законы распределения (см. гл. 4) часто задают в аналитической форме, для чего необходимы какие-то параметры, иначе числовые характеристики, отражающие те или иные стороны этого закона.
Числовые характеристики или параметры распределения случайной величины – характеристики, назначение которых — выразить в
сжатой форме наиболее существенные особенности распределения.
В инженерных расчетах числовые характеристики и операции с ними имеют чрезвычайно важное значение. Очень часто удается решить ту или иную задачу до конца, оставляя в стороне законы распределения и оперируя одними числовыми характеристиками.
В теории вероятностей и математической статистике используются характеристики, имеющие различное назначение и различные области применения. Большинство из них основано на понятии моментов распределения.
Моменты статистического распределения
Понятие моментов в статистических расчетах во многом аналогично понятию моментов в механике, применяемому для описания распределения масс относительно какой-либо точки отсчета..
Моменты статистических распределений могут определяться относительно любой точки отсчета. Однако чаще всего используются моменты двух видов: начальные, определяемые относительно нуля исследуемой величины, и центральные, определяемые относительно среднего значения этой величины.
Начальный момент s-гo порядка дискретной случайной величины X - сумма вида
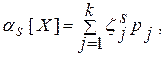
 (3.18)
(3.18)
где ζj — возможные значения X; pj — вероятность появления значения X, равного ζj, k – число возможных значений X;
Начальный момент s-гo порядка непрерывной случайной величины X - интеграл вида
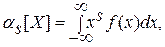
 (3.19)
(3.19)
где f(x) —плотность распределения X.
Первый начальный момент, представляющий собой сумму произведений всех возможных значений случайной величины на их вероятности, называется математическим ожиданием (mx). Для дискретных случайных величин
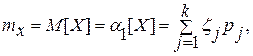
 (3.20)
(3.20)
для непрерывных

 (3.21)
(3.21)
С учетом выражений (3.18) и (3.20) можно записать, что
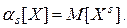
 (3.22)
(3.22)
Отсюда другое определение начального момента:
Начальный момент S-го порядка случайной величины X –математическое ожидание (м. о.) s-й степени этой величины.
Для определения центральных моментов вводится понятие центрированной случайной величины
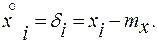 ,
,  (3.23)
(3.23)
представляющей из себя отклонения от математического ожидания
При анализе графиков центрирование аналогично переносу начала координат в среднюю, «центральную», точку, абсцисса которой равна тx. В гидрометеорологических расчетах центрированные величины часто называют отклонениями от среднего или от нормы.
Моменты центрированной случайной величины называются центральными моментами. Они аналогичны моментам относительно центра тяжести в механике.
Центральный момент порядка s случайной величины X –математическое ожидание (м. о.) s-й степени соответствующей центрированной случайной величины
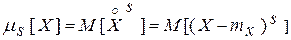
 (3.24)
(3.24)
или, согласно выражению (3.20), для дискретной случайной величины
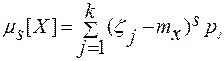
 (3.25)
(3.25)
и с учетом формулы (3.21) для непрерывной случайной величины
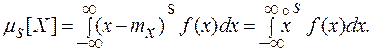
 (3.26)
(3.26)
Второй центральный момент называется дисперсией.
Легко показать, что первый центральный момент равен нулю. Действительно
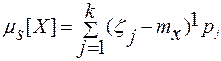 =
= 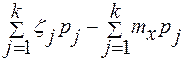 = 0,
= 0,
Точно также можно показать, что нулевой центральный момент равен единице.
В дальнейшем нам понадобятся соотношения, связывающие второй и третий центральный и начальный момент.
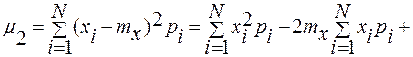

+ 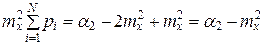
Аналогично для третьего центрального момента

+3 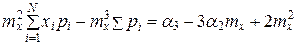 .
.
Таким образом, для начальных и центральных моментов случайной величины характерны следующие соотношения:
μ0 = 1
μ1 = 0
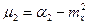 , (3.27)
, (3.27)
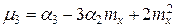 .
.
Числовые характеристики распределения
Числовые характеристики, используемые в практике расчетов, разделяют на характеристики положения, показывающие расположение определенных характеристик распределения на числовой оси X (рис. 3.3.), и характеристики рассеивания.
Из характеристик положения важнейшую роль во всех расчетах играет математическое ожидание mx. (Еще одно возможное обозначений M[X]). Кроме того, часто используются еще две характеристики положения: мода М и медиана Me.
Мода дискретной случайной величины – значение, имеющее наибольшую вероятность.
Для непрерывной случайной величины это определение не подходит, так как вероятности каждого отдельного значения случайной величины равны нулю (см. определение непрерывной случайной величины).
Мода непрерывной случайной величины – значение, имеющее наибольшую плотность вероятности
Наиболее удобно определять моду по многоугольнику или соответственно кривой распределения.
Если многоугольник или кривая распределения имеют более одного максимума (рис. 3.4.а), то распределение называется полимодальным. Иногда встречаются распределения, имеющие посредине не максимум, а минимум (рис 3.4.б). Такое распределение называется амодальным.
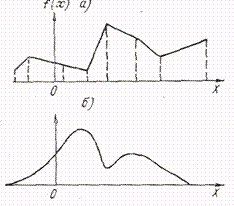
Рис 3.4. Полимодальное распределение
дискретной (а) и непрерывной (б)
случайной величины.
Другая часто применяемая характеристика положения — медиана Me
Медиана случайной величины X – такое ее значение, для которого р(Х < Me) = р(Х > Me), т.е. вероятность значений X, больших и меньших Me, одинакова и, следовательно, равна 0,5.
Геометрически медиана —~ это абсцисса точки, в которой площадь, ограниченная кривой плотности вероятности, делится пополам. Обычно значение Me определяют по функции распределения или обеспеченности.
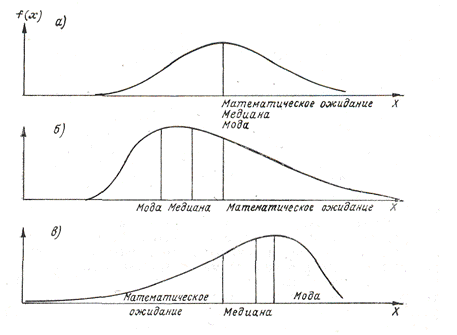
В общем случае математическое ожидание, мода и медиана не совпадают (рис. 3.5), однако в случае симметричного одномодального распределения эти характеристики могут совпадать. В частности, они совпадают для нормального закона распределения.
Другим классом числовых характеристик являются характеристики рассеивания: дисперсия, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии и реже эксцесс.
Дисперсия (см. выше) представляет собой второй центральный момент
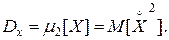
 (3.28)
(3.28)
 .
.
Рис. 3.5 Соотношение между математическим ожиданием, медианой и модой для симметричного распределения (а), распределение с положительной (б) и отрицательной (в) асимметрией
Для непосредственного вычисления дисперсии служат следующие формулы: для непрерывных случайных величин

 (3.29)
(3.29)
для дискретных случайных величин
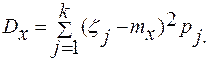 (3.30)
(3.30)
Отсюда определение: дисперсия случайной величины X –математическое ожидание квадрата соответствующей центрированной величины.
Для характеристики рассеивания часто удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Это дает возможность сопоставить рассеивание со значениями самих величин X. В качестве такой величины может служить среднее квадратическое отклонение или стандарт.
Среднее квадратическое отклонение или стандарт – корень квадратный из дисперсии.
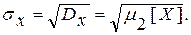
 (3.31)
(3.31)
Для описания заведомо положительных величин большое распространение получила безразмерная характеристика рассеивания — коэффициент вариации
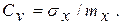
 (3.32)
(3.32)
Коэффициент вариации не зависит от среднего значения и может быть использован для сопоставления изменчивости различных процессов.
Для характеристики симметричности рассеивания значений случайной величины относительно математического ожидания применяется безразмерная величина — коэффициент асимметрии
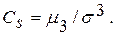
 (3.33)
(3.33)
В соответствии с этой формулой для симметричных распределений, когда каждому + х соответствует -х, кубы х при суммировании уничтожаются и Сs = 0. Асимметрия может быть положительной и отрицательной. Знак асимметрии зависит от соотношения числовых характеристик положения: моды и математического ожидания. Если тх > М, то Сs < 0— положительная асимметрия. Если тх < М — отрицательная асимметрия (см. рис. 3.5).
Примером распределений с положительной асимметрией могут служить ряды концентраций химических элементов в речной воде. В данном случае причиной положительной асимметрии является то, что значения концентраций всегда больше и равны нулю и могут в несколько раз превосходить математическое ожидание. Таким образом, максимум отрицательных отклонений от математического ожидания по абсолютной величине всегда меньше математического ожидания, в то время как положительные отклонения от математического ожидания нередко в несколько раз больше его.
Примером распределений с отрицательной асимметрией могут служить многие ряды максимальных уровней, особенно на участках рек с поймой. Причиной отрицательной асимметрии в данном случае является резкое возрастание ширины живого сечения при выходе воды на пойму.
Для характеристики крутости (островершинности или плоско-вершинности) распределения используется эксцесс, основанный на учете 4-го центрального момента:

 (3.34)
(3.34)
Для нормального закона распределения Ех = 0.
В практических расчетах в формулах математического ожидания (3.20), дисперсии (3.30), среднего квадратического отклонения (3.31), коэффициента вариации(3.32), коэффициента асимметрии (3.33) вместо pj — вероятности появления значения X, равного ζj в N испытаниях – подставляется ее значение по формуле
Pj = m j /N, (3.35)
где mJ число появлений значений X, равных ζj в N испытаниях.
Легко показать, что в этом случае перечисленные формулы принимают следующий вид:
математическое ожидание
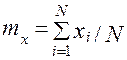 , (3.36)
, (3.36)
дисперсия
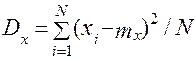 , (3.37)
, (3.37)
среднее квадратическое отклонение
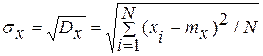 , (3.38)
, (3.38)
коэффициент вариации
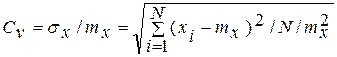 , (3.39)
, (3.39)
коэффициент асимметрии
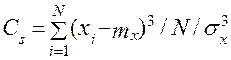 (3.40)
(3.40)
Дата добавления: 2020-10-25; просмотров: 576;











