Общая характеристика законов распределения

Закон распределения случайной величины – всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Законы распределения можно задавать в табличной, графической и аналитической форме. В последнее время широко распространены алгоритмические методы задания.

Простейшей формой задания закона распределения дискретной случайной величины является таблица, называемая рядом распределения, в которой перечислены возможные значения случайной величины ­ζ и соответствующие им вероятности р (табл. 3.1).

Таблица 3.1.

Ряд распределения случайной величины X

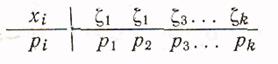
Более наглядной, но менее компактной формой представления закона распределения является графическое изображение, при этом по оси абсцисс откладываются возможные значения случайной величины, а по оси ординат — вероятности этих значений. Для наглядности полученные точки соединяются отрезками прямых линий. Полученная фигура называется многоугольником или полигоном распределения (рис. 3.1).

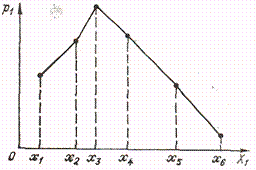
Рис.3.1 – Многоугольник распределения.

Многоугольники распределения могут иметь самую различную форму, однако все они обладают одним общим свойством: сумма ординат многоугольника распределения, представляющая собой сумму вероятностей всех возможных значений случайной величины, всегда равна единице.

Ряд и многоугольник распределения являются исчерпывающими характеристиками дискретной случайной величин. Для непрерывной случайной величины использование этих характеристик невозможно, так как непрерывная величина имеет бесчисленное множество значений, сплошь заполняющих некоторый промежуток (см. выше). Составить таблицу, в которой были бы перечислены все возможные значения такой величины, невозможно. Кроме того, каждое отдельное значение непрерывной слу­чайной величины обычно не обладает никакой отличной от нуля вероятностью.

Для количественного описания закона распределения непрерывной случайной величины используется вероятность события X < х, где х — некоторое значение переменной X. Эта вероятность зависит от х, тоесть является некоторой функцией х, отсюда и название новой характеристики — функция распределения.

Функция распределенияF (х)случайной величины X - вероятность выполнения неравенства X < х при различных значениях х, то есть

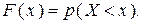(3.4)

Часто функцию распределения называют интегральной функцией распределения или интегральным законом распределения.

Функция распределения — общая форма описания случайной величины, полностью характеризующая ее с вероятностной точки зрения. Она может быть использована как для дискретных, так и для непрерывных случайных величин.

В инженерных расчетах вместо функции распределения принято рассматривать функцию

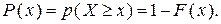
(3.5)

Для отличия от функции распределения, обычно используемой в математической литературе, назовем эту функцию – функцией обеспеченности, а ее графическое изображение — кривой обеспеченности.

Следует отметить некоторые общие свойства функции распределения:

1. Функция распределения F(x) есть неубывающая функция своего аргумента, т. е. при х₂ ≥ x₁

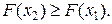
(3.6)

2. На минус бесконечности (х = – ∞) функция распределения равна нулю, т.е

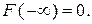
(3.7)

3. На плюс бесконечности (х = ∞.) функция распределения равна единице, т. е.

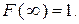
(3.8)

Доказательства перечисленных свойств приводятся в курсе теории вероятностей, например [Гнеденко, Вентцель]. Упрощенное доказательство этих свойств производится с помощью геометрической интерпретации случайной величины в виде случайной точки X на оси ОХ. Точка Х в результате опыта может занять то или иное положение. Во всех случаях функция распределения F(x) есть вероятность того, что случайная точка Х будет находиться левее заданного х.

Будем увеличивать X, т.е. перемещать точку х вправо по оси ОХ. Очевидно, что с увеличением области значений Х по числовой оси ОХ, вероятность попадания Х в эту область не может уменьшаться, она или возрастает, или остается неизменной.

Будем дальше смещать точку х вправо по оси ОХ. Вместе с этим будет возрастать область возможных значений Х и в пределе при х = ∞ все возможные значения Х окажутся левее х, т.е. события Х<х станут достоверными. Отсюда вероятность значений Х<∞, т.е. функция распределения при х = +∞ F(X<∞) равна единице.

Аналогично, перемещая точку х влево, получаем, что F(X = ‑∞) = 0.

Исходя из этих свойств можно получить общее представление о графике функции распределения. Очевидно, он должен представлять собой график неубывающей функции, значения которой начинаются от 0 и доходят до 1 (рис. 3.2).

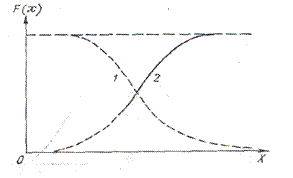
Рис.3.2 График функции

обеспеченности (1) и распределения (2).

Можно показать, что для функции обеспеченности, установленные выше соотношения будут иметь обратный вид.

1. Функция обеспеченности Р(х) есть убывающая (точнее, невозраcтающая) функция своего аргумента, т.е. при х₂>х₁ Р(х₂)≤P(x₂).

2. При х = ‑∞ функция обеспеченности равна единице, т.е. Р(‑∞) = 1.

3. При х = ∞ функция обеспеченности равна нулю, т.е. Р(+∞) = 0.

Исходя из этого очевидно, что кривая обеспеченности симметрична кривой функции распределения и пересекается с ней при F(x) = Р(х) = 0,5 (рис. 3.2).

По известным функциям распределения или обеспеченности может быть установлена вероятность появления случайной величины в заданном интервале, полузамкнутом слева. Как следует из курса теории вероятностей, она равна разности значений функции распределения в концах интервала,

т. е.

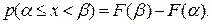
(3.9)

Тогда из выражения (3.5) также следует, что

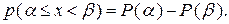(3.10)

Часто событие, заключающееся в появлении случайной вели­чины в интервале (α, β), называют попаданием случайной величины на заданный участок.

Функция распределения случайной величины является ее исчерпывающей характеристикой, но по ней трудно судить о характере распределения случайной величины в небольшой окрестности той или другой точки числовой оси. Для дискретной случайной величины с этой целью можно воспользоваться многоугольником или полигоном распределения. Для непрерывной случайной величины наглядное представление дает функция, называемая плотностью распределения вероятности или дифференциальным законом рас­пределения.

Плотность распределения - производная функции распределения вероятностей

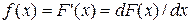(3.11)

в тех точках, где она существует.

Кривая, изображающая плотность распределения случайной величины, называется кривой распределения.

Понятие плотности вероятности можно обобщить и на дискретные случайные величины, если воспользоваться дельта-функцией Дирака δ(х)

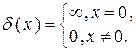
(3.12)

Так, для дискретной случайной величины, закон распределения которой задан рядом распределения x_j, (j=1, N), плотность вероятности определяется по формуле

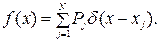
(3.13)

Таким образом, плотность дискретной случайной величины равна нулю всюду, кроме точек х₁, х₂, . . ., x_N, в которых она «делает всплески в бесконечность», причем «площади всплесков» в точках x₁ х₂ ,. . ., x_n равны соответственно р₁, р₂ …, p_N.

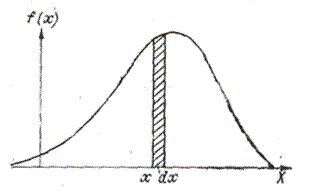Рассмотрим непрерывную случайную величину X с плотностью вероятности f(x). Вероятность попадания случайной величины X на элементарный участок dx, примыкающий к точке X (рис. 3.3), с точностью до бесконечно малых высшего порядка равна f(x)dx. Величина f(x)dx называется элементом вероятности. Геометрически — это площадь элементарного прямоугольника, опирающегося на отрезок dx (рис. 3.3).

Рис.3.3 Кривая распределения и элемент вероятности.

Вероятность попадания значений х на отрезок от α до β, очевидно, будет равна сумме элементов вероятности на всем этом участке, т. е.

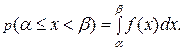
(3.14)

Геометрически вероятность попадания значений X на участок (α, β) равна площади под кривой распределения, опирающейся на этот участок (см. рис. 3.3).

Теперь выразим функцию распределения через плотность вероятности. По определению F(x) = р (X < х) = р (-∞ ≤X < х). Отсюда с учетом формулы (3.14)

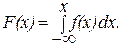
(3.15)

Геометрически функция распределения, очевидно, есть площадь. кривой распределения, лежащая левее точки X.

Основные свойства плотности распределения.

1. Плотность распределения есть неотрицательная функция, т. е..

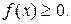
(3.16)

Это свойство является следствием того, что функция распреде­ления есть неубывающая функция. Поэтому числитель выражения плотности вероятности (3.11) больше или равен нулю, а знамена­тель (Δх_i = x_i — x_i-1) тоже положителен.

2. Интеграл в бесконечных пределах от плотности распределе­ния равен единице:

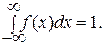
(3.17)

Это следует из формулы (3.15) и из того, что F(x = ∞) = 1. Геометрически (см. рис. 3.3) основные свойства плотности распре­деления означают, что вся кривая распределения лежит не ниже оси абцисс, и полная площадь, ограниченная кривой распределе­ния и осью абсцисс, равна единице.